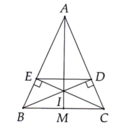
Cho tam giác ABC cân tại A kẻ BD vuông góc với AC (D thuộc AC) CE vuông góc với AB (E thuộc AB)
C/minh
BD=CE
Tam giác ADE cân
DE song song với BC
Gọi I là giao điểm của BD và CE
C/minh tam giác BIE bằng tam giác CID , tam giác BIE là tam giác gì?
Gọi D là trung điểm BC c /minh A I D thẳng hàng



a, Xét \(\Delta ABD\) và \(\Delta ACE\) vuông tại \(D;E\) có:
\(AB=AC\left(\Delta ABC-cân\right)\)
\(\widehat{A}\) chung
\(\Rightarrow\Delta ABD=\Delta ACE\left(ch-gn\right)\left(1\right)\)
\(\Rightarrow BD=CE\left(2c.t.ứ\right)\)
b, Từ \(\left(1\right)\Rightarrow AD=AE\left(2c.t.ứ\right)\)
\(\Rightarrow\Delta ADE\) cân tại \(A\)
\(\Rightarrow\widehat{ADE}=\frac{180^0-\widehat{A}}{2}\left(2\right)\)
Ta có: \(\Delta ABC\) cân tại \(A\)
\(\Rightarrow\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\left(3\right)\)
c, Từ \(\left(3\right)\left(2\right)\Rightarrow\widehat{AED}=\widehat{ABC}\)
Mà 2 góc đang ở vị trí đồng vị nên:
\(\Rightarrow DE//BC\)
d, Xét \(\Delta EIB\) và \(\Delta DIC\) vuông tại \(E;D\) có:
\(EB=DC\left(AB=AC;EA=DA\right)\)
\(\widehat{EIB}=\widehat{DIC}\left(đ.đỉnh\right)\)
\(\Rightarrow\Delta EIB=\Delta DIC\left(cgv-gnđ\right)\left(4\right)\)
e, Xét \(\Delta BIE\) có:
\(\widehat{BEI}=90^0\)
\(\Rightarrow\Delta BIE\) vuông tại \(E\)
f, Từ \(\left(4\right)\Rightarrow BI=CI\left(2c.t.ứ\right)\left(5\right)\)
Ta có: \(BM=CM\left(M-là-t.điểm-BC\right)\)
\(\Rightarrow D\in\) đường trung trực \(BC\left(6\right)\)
Từ \(\left(5\right)\Rightarrow I\in\) đường trung trực \(BC\left(7\right)\)
Và \(AB=AC\Rightarrow A\in\) đường trung trực \(BC\left(8\right)\)
Từ \(\left(6\right)\left(7\right)\left(8\right)\Rightarrow A;I;M\) thẳng hàng.
P/s: Sửa đề Gọi \(M\) là trung điểm \(BC\)
Nếu nhưu gọi \(D\) thì nó bị trùng rồi bạn.
Có gì không hiểu thì hỏi ^_^