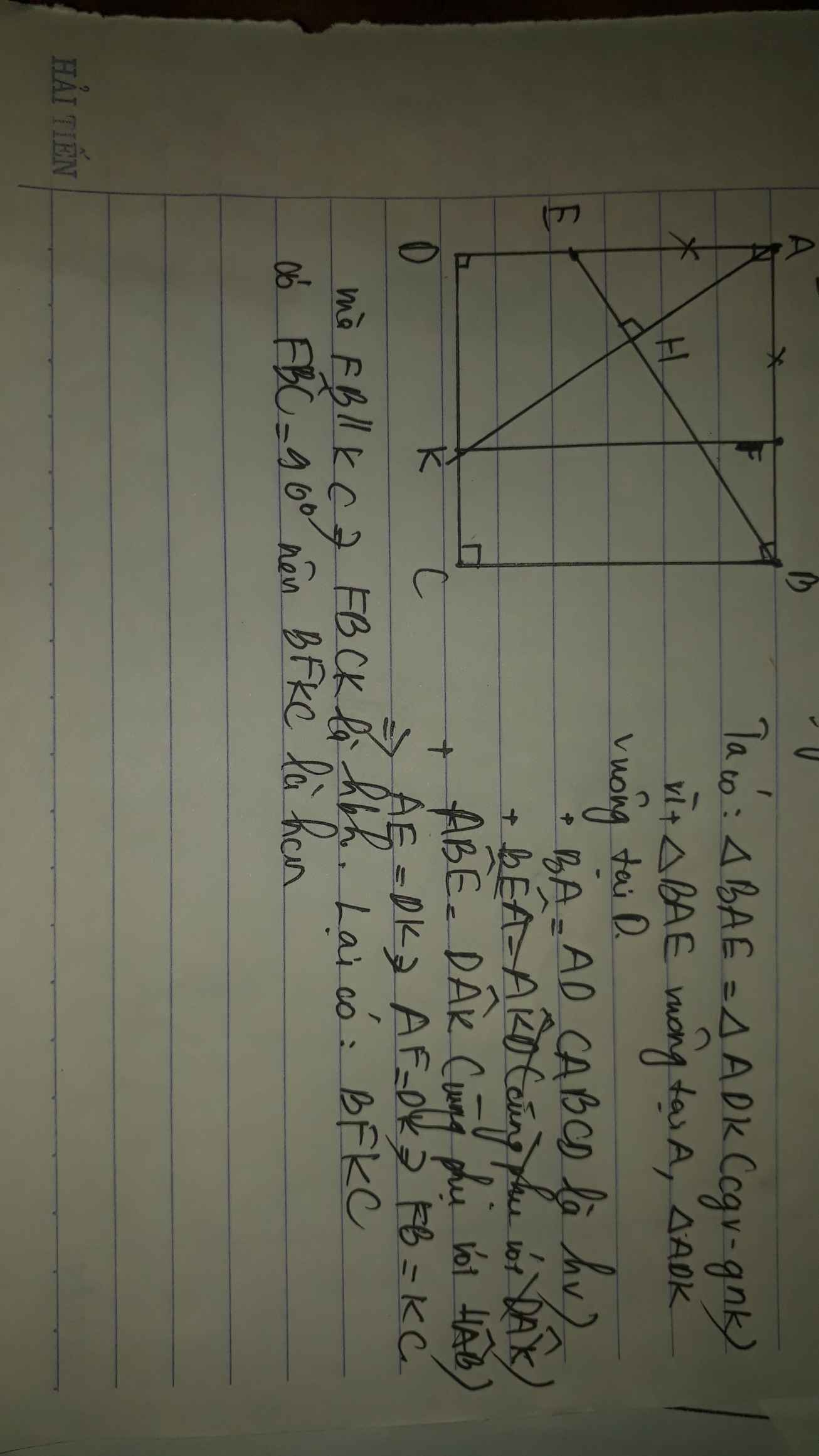
Cho hình vuông ABCD, trên AB và AD lần lượt lấy I, E sao cho AI=AE. H là hình chiếu của A trên DI, M là giao điểm AH và BC. Chứng minh rằng AM=DI.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trả lời:
a, Gọi O là giao điểm 2 đường chéo của hình chữ nhật ABCD
=> O là trung điểm của BD và AC
Xét tam giác ACE có:
O là trung điểm của AC
M là trung điểm của AE ( gt )
=> OM là đường trung bình của tam giác ACE
=> OM // CE
hay BD // CE
=> ^BDC = ^ECK ( 2 góc đồng vị ) (1)
Vì O là trung điểm của BD và AC
=> OD = BD/2 và OC = AC/2
Mà BD = AC ( ABCD là hình chữ nhật )
=> OD = OC
=> tam giác DOC cân tại O
=> ^BDC = ^ACD (tc) (2)
Xét tứ giác HEKC có:
^EHC = 90o
^HCK = 90o
^EKC = 90o
=> tứ giác HEKC là hình chữ nhật ( dh1)
Gọi I là giao điểm 2 đường chéo của hình chữ nhật HEKC
=> I là trung điểm của CE và HK
=> IC = CE/2 và IK = HK/2
Mà CE = HK ( HEKC là hình chữ nhật )
=> IC = IK
=> tam giác ICK cân tại I
=> ^ECK = ^IKC (tc) (3)
Từ (1) (2) và (3) => ^ACD = ^IKC
Mà 2 góc này ở vị trí đồng vị
nên AC // HK ( đpcm )
b, Xét tam giác ACE có:
I là trung điểm của CE
M là trung điểm của AE (gt)
=> IM là đường trung bình của tam giác ACE
=> IM // AC
Mà HK // AC ( cm ở ý a ) và H, I, K thẳng hàng
nên M, H, K thẳng hàng ( đpcm )
k nha đúng

\(a)\) Xét tam giác vuông ADM và tam giác vuông BAF có :
\(AD=AB\) ( do ABCD là hình vuông )
\(\widehat{DAM}=\widehat{ABF}\) \(\left(=90^0-\widehat{BAF}\right)\)
Do đó : \(\Delta ADM=\Delta BAF\) ( cạnh góc vuông - góc nhọn )
Suy ra : \(DM=AF\) ( 2 cạnh tương ứng )
Mà \(AE=AF\)(GT) \(\Rightarrow\)\(DM=AE\)
Tứ giác AEMD có : \(DM=AE\)\(;\)\(DM//AE\) ( do \(AB//CD\) ) và có \(\widehat{ADC}=90^0\) nên AEMD là hình chữ nhật
Vậy AEMD là hình chữ nhật
\(b)\) Xét \(\Delta HAB\) và \(\Delta HFA\) có :
\(\widehat{ABH}=\widehat{FAH}\) ( do \(\widehat{ABF}=\widehat{DAM}\) theo câu a ) *(góc DÂM -_- haha)*
\(\widehat{BHA}=\widehat{AHF}\) \(\left(=90^0\right)\)
Do đó : \(\Delta HAB~\Delta HFA\) \(\left(g-g\right)\)
Suy ra : \(\frac{HB}{AH}=\frac{AB}{AF}\) ( các cặp cạnh tương ứng tỉ lệ )
Mà \(AB=BC;AF=AE\left(=DM\right)\) nên \(\frac{HB}{AH}=\frac{BC}{AE}\)
Lại có : \(\widehat{HAB}=90^0-\widehat{FAH}=90^0-\widehat{ABH}=\widehat{HBC}\)\(\Rightarrow\)\(\widehat{HAB}=\widehat{HBC}\)
Xét \(\Delta CBH\) và \(\Delta EAH\) có :
\(\frac{HB}{AH}=\frac{BC}{AE}\)
\(\widehat{HAB}=\widehat{HBC}\)
Do đó : \(\Delta CBH~\Delta EAH\) \(\left(c-g-c\right)\)
Vậy \(\Delta CBH~\Delta EAH\)
\(c)\) \(\Delta ADM\) có \(CN//AD\) và cắt \(AM;DM\) nên theo hệ quả định lý Ta-let ta có :
\(\frac{CN}{AD}=\frac{MN}{AM}\)\(\Leftrightarrow\)\(\frac{AD}{AM}=\frac{CN}{MN}\)\(\Leftrightarrow\)\(\frac{AD^2}{AM^2}=\frac{CN^2}{MN^2}\) \(\left(1\right)\)
\(\Delta ABN\) có \(CM//AB\) và cắt \(AN;BN\) nên theo hệ quả định lý Ta-let ta có :
\(\frac{MN}{AN}=\frac{MC}{AB}\) hay \(\frac{MN}{AN}=\frac{MC}{AD}\)\(\Leftrightarrow\)\(\frac{AD}{AN}=\frac{MC}{MN}\)\(\Leftrightarrow\)\(\frac{AD^2}{AN^2}=\frac{MC^2}{MN^2}\) \(\left(2\right)\)
Từ (1) và (2) suy ra : \(\frac{AD^2}{AM^2}+\frac{AD^2}{AN^2}=AD^2\left(\frac{1}{AM^2}+\frac{1}{AN^2}\right)=\frac{CN^2}{MN^2}+\frac{MC^2}{MN^2}=\frac{CN^2+MC^2}{MN^2}=\frac{MN^2}{MN^2}=1\)
\(\Rightarrow\)\(\frac{1}{AM^2}+\frac{1}{AN^2}=\frac{1}{AD^2}\) ( đpcm )
Vậy \(\frac{1}{AD^2}=\frac{1}{AM^2}+\frac{1}{AN^2}\)

a: Xét ΔAED vuông tại A và ΔHAD vuông tại H có
góc D chung
=>ΔAED đồng dạng với ΔHAD
=>AE/AH=AD/DH
=>AE*DH=AH*AD
b: AH/AE=DH/AD
=>AH/AE=DH/DC
=>AH/DH=AF/DC
=>ΔAHF đồng dạng với ΔDHC

Bạn xem lại đề nhé. K là giao điểm của AH và CD, BFKC là hcn