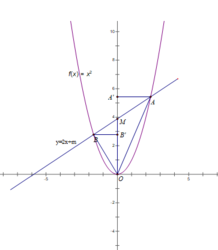
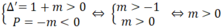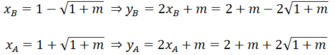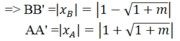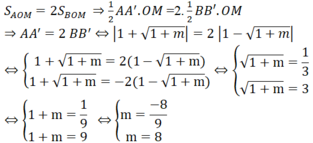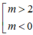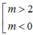Trong mặt phẳng toạ độ Oxy cho (P)y=mx^2(m>0) và đường thẳng (d)y=2x-m^2 a) Tìm m để (d) cắt (P) tại hai điểm phân biệt A,B.Cmr A và B nằm cùng về một phía của trục tung b) Với m tìm được ở câu a.Gọi xA,xB lần lược là hoành đồ điểm A và B.Tìm m để (P)=2/(xA+xB)+1/(4xAxB+1) đạt GTNN Giúp mk với ạ!!!!!Mk đang cần gấp Mk cảm ơn trước!!!