Áp dụng quy tắc đổi dấu để các phân thức có cùng mẫu thức rồi thực hiện phép cộng phân thức:
a) \(\frac{16+x}{x^2-2x}+\frac{18}{2x-x^2}\)
b)\(\frac{2y}{2x^2-xy}+\frac{4x}{xy-2x^2}\)
c)\(\frac{4-x^2}{x-3}+\frac{2x-2x^2}{3-x}+\frac{5-4x}{x-3}\)
Mong 500 ae giúp ạ ^^

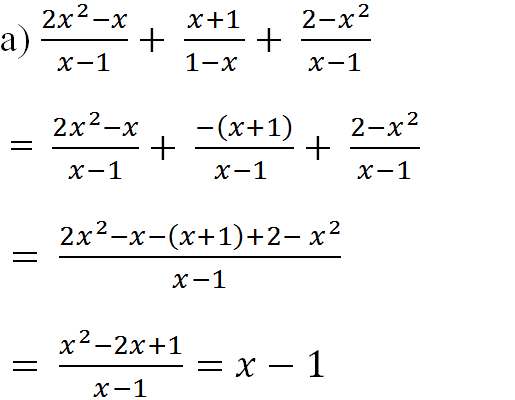
\(=\frac{16+x}{x^2-2x}-\frac{18}{x^2-2x}\)
\(=\frac{16+x-18}{x\left(x-2\right)}\)
\(=\frac{-2+x}{x\left(x-2\right)}\)
a) \(\frac{16+x}{x^2-2x}+\frac{18}{2x-x^2}=\frac{16+x-18}{x^2-2x}=\frac{x-2}{x\left(x-2\right)}=\frac{1}{x}\)
b) \(\frac{2y}{2x^2-xy}+\frac{4x}{xy-2x^2}=\frac{2y-4x}{2x^2-xy}=\frac{-2\left(2x-y\right)}{x\left(2x-y\right)}=\frac{-2}{x}\)
c) \(\frac{4-x^2}{x-3}+\frac{2x-2x^2}{3-x}+\frac{5-4x}{x-3}=\frac{4-x^2+2x^2-2x+5-4x}{x-3}=\frac{x^2-6x+9}{x-3}=\frac{\left(x-3\right)^2}{x-3}=x-3\)