Cho tam giác ABC có \(\widehat{A}\)= 75 độ; \(\widehat{B}\)= 65 độ. Tia phân giác AD cắt BC tại D. Tính \(\widehat{ADB;ADC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
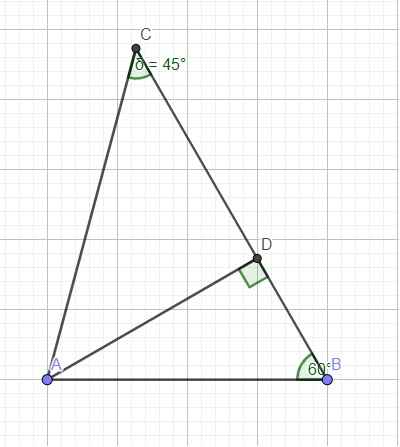
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)
HM
10 tháng 7 2017
trời ạ
ta có tam giác ABC= tam giác DEF
suy ra góc A = góc D , góc b = góc E , góc C = góc F
trong tam giác ABC CÓ góc A + góc B +góc C = 180 độ
mà góc A=55 độ , B = 75 độ
suy ra góc C =50 độ
mà góc C = góc F = 50 độ
góc D = góc A =55 độ
góc B = góc E = 75 độ
cho mình nha
thanhks
10 tháng 7 2017
giải
Ta có : \(\Delta ABC=\Delta DEF\)
\(\Rightarrow\widehat{A}=\widehat{D}=55^0\)
\(\widehat{B}=\widehat{E}=75^0\)
Ta có tổng 3 góc trong một tam giác bằng 1800
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{C}=180^0-\left(\widehat{A}+\widehat{B}\right)=180^0-\left(55^0+75^0\right)\)
\(\Rightarrow\widehat{C}=\widehat{F}=50^0\)
Ta có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^O\)
\(\Rightarrow\widehat{C}=180^O-\widehat{A}-\widehat{B}\)
\(\Rightarrow\widehat{C}=180-75-65=40\)
Vì AD là tia phân giác của góc A
\(\Rightarrow\hept{\begin{cases}A_1=37,5\\A_2=37,5\end{cases}}\)
Ta có
\(A_1+C+D_1=180\)
\(\Rightarrow D_1=180-C-A_1\)
\(\Rightarrow D_1=180-40-37,5=102,5^O\)
Tương tự \(\Delta ABD\)ta có
\(D_1=77,5^o\)
Vậy......