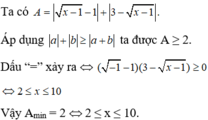tìm giá trị nhỏ nhất của biểu thức sau : A = 2x^2 + 6x - 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
O0
1
1 tháng 11 2019
A = 2x2 + 6x - 1
A = 2( x2 + 3x - 1 / 2 )
A = 2[ x2 + 2 . 3 / 2 . x + ( 3 / 2 )2 - ( 3 / 2 )2 - 1 / 2 ]
A = 2[ ( x + 3 / 2 )2 - 11 / 4 ]
A = ( x + 3 / 2 )2 - 11 / 2 \(\ge\)- 11 / 2
Dấu " = " xảy ra\(\Leftrightarrow\)x + 3 / 2 = 0
\(\Rightarrow\)x = 3 / 2
Min A = - 11 / 2 \(\Leftrightarrow\)x = 3 / 2
20 tháng 7 2021
a, \(A=-x^2-2x+3=-\left(x^2+2x-3\right)=-\left(x^2+2x+1-4\right)\)
\(=-\left(x+1\right)^2+4\le4\)
Dấu ''='' xảy ra khi x = -1
Vậy GTLN là 4 khi x = -1
b, \(B=-4x^2+4x-3=-\left(4x^2-4x+3\right)=-\left(4x^2-4x+1+2\right)\)
\(=-\left(2x-1\right)^2-2\le-2\)
Dấu ''='' xảy ra khi x = 1/2
Vậy GTLN B là -2 khi x = 1/2
c, \(C=-x^2+6x-15=-\left(x^2-2x+15\right)=-\left(x^2-2x+1+14\right)\)
\(=-\left(x-1\right)^2-14\le-14\)
Vâỵ GTLN C là -14 khi x = 1
Bài 8 :
b, \(B=x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\)
Dấu ''='' xảy ra khi x = 3
Vậy GTNN B là 2 khi x = 3
c, \(x^2-x+1=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu ''='' xảy ra khi x = 1/2
Vậy ...
c, \(x^2-12x+2=x^2-12x+36-34=\left(x-6\right)^2-34\ge-34\)
Dấu ''='' xảy ra khi x = 6
Vậy ...
PT
1
NT
1. Tìm giá trị nhỏ nhất của biểu thức P= 2x2 - 6x
2. Tìm giá trị lớn nhất của biểu thức E=4x - x2 + 3
3
9 tháng 1 2017
ta có
P = 2x^2 - 6x
= 2( x^2 - 3x + 9/4) - 9/4
= 2( x-3/2)^2 - 9/4
nhận xét 2(x-3/2)^2 >=0
=> 2(x-3/2)^2 - 9/4 >=-9/4
dấu = xảy ra khi và chỉ khi
x- 3/2 = 0
=> x= 3/2
9 tháng 1 2017
4x - x^2 + 3
= -x^2 + 4x - 4 +7
= -(x^2 - 4x + 4) + 7
= -(x-2)^2 + 7
nhận xét -(x-2)^2 <=0
=> -(x-2)^2 + 7 <=7
đấu = xảy ra khi và chỉ khi
x-2 = 0
=> x= 2
PT
2
23 tháng 7 2017
\(A=2x^2+9y^2-6xy-6x-12y+2046\)
\(=\left[\left(x^2-6xy+9y^2\right)+\left(4x-12y\right)+4\right]-4+\left(x^2-10x+25\right)-25+2046\)
\(=\left[\left(x-3y\right)^2+4\left(x-3y\right)+4\right]+\left(x-5\right)^2-4-25+2046\)
\(=\left(x-3y+2\right)^2+\left(x-5\right)^2+2017\ge2017\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x-3y+2=0\\x-5=0\end{cases}\Leftrightarrow\hept{\begin{cases}y=\frac{7}{3}\\x=5\end{cases}}}\)
Vậy \(A_{min}=2017\) tại \(x=5;y=\frac{7}{3}\)
TN
26 tháng 7 2016
2x^2-6x+1
\(=2\left(x^2-3x+\frac{1}{2}\right)\)
\(=2\left(x^2-3x+\frac{9}{4}\right)-\frac{7}{2}\)
\(=2\left(x-\frac{3}{2}\right)^2-\frac{7}{2}\ge0-\frac{7}{2}=-\frac{7}{2}\)
Dấu = khi 2(x-3/2)2=0 <=>x=3/2
Vậy Hmin=7/2 khi x=3/2
NV
26 tháng 7 2016
\(2x^2-6x+1=2\left(x^2-3x+\frac{1}{2}\right)\)
\(=2\left[x^2+2.\frac{3}{2}.x+\left(\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+\frac{1}{2}\right]\)
\(=2\left[\left(x+\frac{3}{2}\right)^2-\frac{7}{4}\right]\)
\(=2\left(x+\frac{3}{2}\right)^2-\frac{7}{2}\ge-\frac{7}{2}\)
Vậy Min đề = -7/2 khi x + 3/2 = 0 => x = -3/2
PN
2
18 tháng 3 2018
\(A=\frac{2x^2-6x+5}{x^2-2x+1}=\frac{x^2-4x+4+x^2-2x+1}{x^2-2x+1}\)
\(=\frac{\left(x-2\right)^2+\left(x-1\right)^2}{\left(x-1\right)^2}=\frac{\left(x-2\right)^2}{\left(x-1\right)^2}+1\)
Vì \(\hept{\begin{cases}\left(x-2\right)^2\ge0\\\left(x-1\right)^2\ge0\end{cases}}\)\(\Rightarrow\frac{\left(x-2\right)^2}{\left(x-1\right)^2}\ge0\)\(\Rightarrow\frac{\left(x-2\right)^2}{\left(x-1\right)^2}+1\ge1\)
\(\Rightarrow A\ge1\).Nên GTNN của \(A=1\) đạt được khi \(x=2\)
23 tháng 10 2020
A = x2 - 2x + 9 = ( x2 - 2x + 1 ) + 8 = ( x - 1 )2 + 8 ≥ 8 ∀ x
Dấu "=" xảy ra khi x = 1
=> MinA = 8 <=> x = 1
B = x2 + 6x - 3 = ( x2 + 6x + 9 ) - 12 = ( x + 3 )2 - 12 ≥ -12 ∀ x
Dấu "=" xảy ra khi x = -3
=> MinB = -12 <=> x = -3
C = ( x - 1 )( x - 3 ) + 9 = x2 - 4x + 3 + 9 = ( x2 - 4x + 4 ) + 8 = ( x - 2 )2 + 8 ≥ 8 ∀ x
Dấu "=" xảy ra khi x = 2
=> MinC = 8 <=> x = 2
D = -x2 - 4x + 7 = -( x2 + 4x + 4 ) + 11 = -( x + 2 )2 + 11 ≤ 11 ∀ x
Dấu "=" xảy ra khi x = -2
=> MaxD = 11 <=> x = -2
