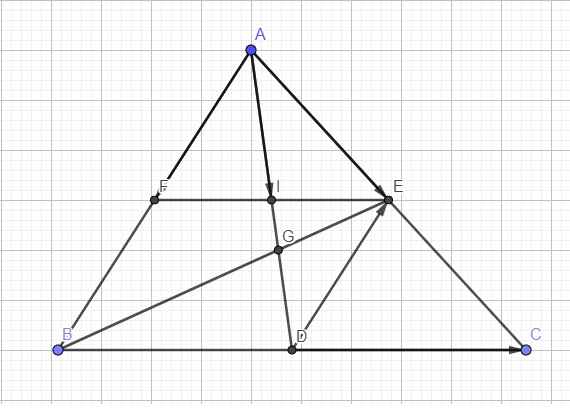
Cho tam giác ABC trọng tâm G, I là trung điểm BC hãy xác định tổng của 2 vécto AI+GI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do G là trọng tâm tam giác ABC nên tọa độ G:
x G = x A + x B + x C 3 = − 1 + 5 + 0 3 = 4 3 y G = y A + y B + y C 3 = 1 + ( − 3 ) + 2 3 = 0 ⇒ G 4 3 ; 0
Điểm G1 là điểm đối xứng của G qua trục Oy nên G 1 − 4 3 ; 0
Đáp án D

F là trung điểm AB \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AB}\) ; E là trung điểm AC \(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AC}\)
Ta có EF song song BC (đường trung bình)
Mà D là trung điểm BC \(\Rightarrow\) I là trung điểm EF \(\Rightarrow AI\) là trung tuyến tam giác AEF
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AE}+\dfrac{1}{2}\overrightarrow{AF}\)
Theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{2}{3}\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=\dfrac{2}{3}\overrightarrow{AE}+\dfrac{2}{3}\overrightarrow{AF}\)
DE là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{BA}=-\dfrac{1}{2}\overrightarrow{AB}=-\overrightarrow{AE}\) hay \(\overrightarrow{DE}=-\overrightarrow{AE}+0.\overrightarrow{AF}\)
D là trung điểm BC \(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=-\overrightarrow{AE}+\overrightarrow{AF}\)