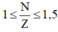1 nguyên tố thuộc nhóm VIA có tổng số proton, notron, và electron trong nguyên tử là 24. cấu hình electron nguyên tử của nguyên tố đó là gì
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 8 2017
Nguyên tố thuộc nhóm VIIA nên có 7e lớp ngoài cùng:
Cấu hình electron: 1s22s22p5.
TP
Thảo Phương
CTVVIP
28 tháng 6 2021
Ta có: \(1\le\dfrac{N}{Z}\le1,5\)
\(\Rightarrow Z\le N\le1,5Z\)
\(\Rightarrow3Z\le2Z+N\le3,5Z\)
Vậy ta có : \(3Z\le24\le3,5Z\)
=> \(6,86\le Z\le8\)
=>\(\left[{}\begin{matrix}Z=7\left(N\right)\\Z=8\left(O\right)\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}N=10\\N=8\end{matrix}\right.\)
Mà theo đề bài : \(1\le\dfrac{N}{Z}\le1,5\)
=> Chỉ có O thỏa mãn
=> Z là O , số P= số E =8 , N=8
b) Cấu hình E: 1s22s22p4
26 tháng 1 2017
Nguyên tố cần tìm thuộc nhóm VIIA → nguyên tử có 7e ở lớp ngoài cùng. Vì lớp thứ nhất chỉ chứa tối đa 2e nên nguyên tử của nguyên tố này phải có ít nhất 2 lớp electron (n ≥ 2).
+ Nếu n = 2, có 2 lớp e, số e ở các lớp là : 2,7 → nguyên tử gồm : 9p, 9e và 10n (tổng số hạt là 28, phù hợp đề bài).
+ Nếu n = 3, có 3 lớp e, số e ờ các lớp là : 2, 8, 7 → vậy chỉ riêng số p + số e = 17 + 17 = 34 > 28 → trái với đề bài. Vậy nguyên tố cần tìm có z = 9 với cấu hình electron : 1 s 2 2 s 2 2 p 5
H
5 tháng 9 2021
a) Gọi số proton, số notron của X là p, n
Số p = Số e
Tổng số hạt trong X: 2p + n = 24 → n = 24 - 2p
Ta có: p ≤ n ≤ 1,52p → p ≤ 24 - 2p ≤ 1,52p
→ 6,8 ≤ p ≤ 8
→ p = 7 hoặc p = 8
Vì X thuộc nhóm VIA nên p = 8
X (Z = 8): $1s^22s^22p^4$
