Gọi A,B là giao điểm của hai đường tròn (C1) và (C2).Trong đá các đường tròn(C1),(C2) lần lượt có phương trình x2+y2-2x-4y+1=0 và x2+y2-4x=0 phương trình đường thẳng AB là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 5 2018
Đáp án D
- Ta có :
(C1) tâm I1(0;2) và R1= 3; (C2) tâm I2( 3;-4) và R2= 3
- Nhận xét : 
không cắt C2
- Gọi d: ax+ by+ c= 0 là tiếp tuyến chung , thế thì : d(I1; d) = R1 và d (I2; d) = R2
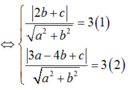
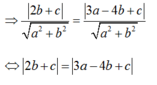
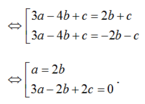
- Trường hợp: a= 2b thay vào (1):
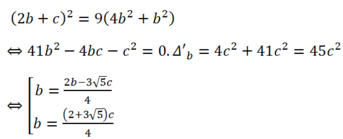
- Do đó ta có hai đường thẳng cần tìm :
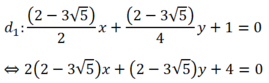
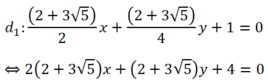
- Trường hợp :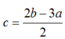 
thay vào :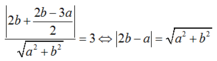 
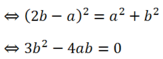
-Có 2 đường thẳng : d3: 2x- 1 = 0 và d4: 6x + 8y -1= 0.
Có tất cả 4 tiếp tuyến chung.
CM
12 tháng 4 2019
Tọa độ giao điểm là nghiệm của hệ phương trình
x 2 + y 2 − 6 x − 4 y + 9 = 0 x 2 + y 2 − 2 x − 8 y + 13 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 − 4 x + 4 y − 4 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 ( 1 ) x − y + 1 = 0 ( 2 )
Từ (2) suy ra: y = x+ 1 thay vào (1) ta được:
x 2 + ( x + 1 ) 2 - 6 x – 4 ( x + 1 ) + 9 = 0 x 2 + x 2 + 2 x + 1 - 6 x - 4 x – 4 + 9 = 0
2 x 2 – 8 x + 6 = 0
Vậy 2 đường tròn đã cho cắt nhau tại 2 điểm là (1; 2) và (3;4).
ĐÁP ÁN B
CM
27 tháng 4 2019
Tọa độ giao điểm của 2đường tròn đã cho thỏa mãn hệ phương trình:
⇔
⇔
⇔
⇔
⇔
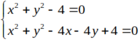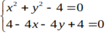
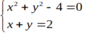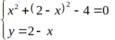
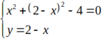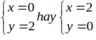
Vậy giao điểm A(0; 2) và B( 2;0).
Chọn C.
CM
22 tháng 11 2019
Tạo độ giao điểm của 2 dường tròn thỏa mãn hệ phương trình:
⇔
⇔
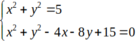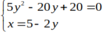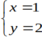
Vậy toạ độ giao điểm là A( 1; 2) .
Chọn B.
CM
22 tháng 5 2017
ĐÁP ÁN D
Tọa độ giao điểm của đường thẳng ∆ và đường tròn (C) nếu có là nghiệm hệ phương trình: là nghiệm của hệ phương trình
x − y + 4 = 0 ( 1 ) x 2 + y 2 + 2 x − 4 y − 8 = 0 ( 2 )
Từ (1) suy ra: y = x + 4 thay vào (2) ta được:
x 2 + ( x + 4 ) 2 + 2 x – 4 . ( x + 4 ) - 8 = 0 x 2 + x 2 + 8 x + 16 + 2 x - 4 x – 16 - 8 = 0
2x2 + 6x - 8 = 0 ⇔ x = 1 ⇒ y = 5 x = − 4 ⇒ y = 0
Vậy đường thẳng cắt đường tròn tại 2 điểm phân biệt là (1; 5) và ( -4; 0)
CM
27 tháng 6 2019
Đường tròn C 1 có tâm I 1 1 ; 2 và bán kính R 1 = 1 .
Đường tròn C 2 có tâm I 2 - 1 ; 0 và bán kính R 2 = 1 .
Chọn B
