Cho tam giác ABC, lấy điểm M bất kì thuộc cạnh BC. Gọi (O1) là đường tròn đi qua hai điểm A,M đồng thời tiếp xúc với AC. Định nghĩa tương tự với (O2). Gọi BX,CY lần lượt là tiếp tuyến thứ hai kẻ từ B và C đến (O2) và (O1). Chứng minh rằng đường tròn (MXY) tiếp xúc với BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


If mày định trình bày một idea nào đó, mày should dùng brain của mày

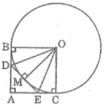
Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)

1: I là tâm đường tròn nội tiếp
QB=QC
=>QB=QI
=>ΔQBI cân tạiQ
2: Xet ΔAMI và ΔANI có
góc AMI=góc ANI
góc MAI=góc NAI
AI chung
=>ΔAMI=ΔANI
=>góc AMN=góc ANM=90 độ-1/2*góc ABC và AM=AN
=>góc EMB=góc NMB=90 độ+1/2*gócc ABC
góc IBC=1/2*góc ABC
góc ICB=góc ACB/
=>góc EIB+góc EMB=180 độ
=>ĐPCM

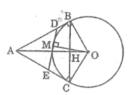
Áp dụng định lí Pitago vào tam giác vuông ABO, ta có:
A O 2 = A B 2 + B O 2
Suy ra: A B 2 = A O 2 - B O 2 = 5 2 - 3 2 = 16
AB = 4 (cm)
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
AD + DE + EA = AD + DB + AE + EC
= AB + AC = 2AB = 2.4 = 8 (cm)

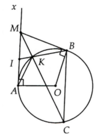
a, ∆IAK:∆IBA => I A I B = I K I A
Mà IA = IM => I M I B = I K I M
=> ∆IKM:∆IMB
b, Chứng minh được: I M K ^ = K C B ^ => BC//MA(đpcm)
Dựng một đường tròn đi qua M và X đồng thời tiếp xúc với BC, đường tròn đó cắt (O1) tại Y' khác M.
Gọi Y'M và XM cắt đường tròn (AXY') lần lượt tại K và L (K khác Y'; L khác X); BC cắt (O1);(O2) tại P,Q; QX cắt PY' tại N
Ta có ^AXN = 1800 - ^AXQ = 1800 - ^AMQ = ^AMP = ^AY'N, suy ra N thuộc đường tròn (AXY')
Do vậy ^AKM = ^ANP mà ^AMK = ^APN nên \(\Delta\)KAM ~ \(\Delta\)NAP (g.g) suy ra AK.AP = AM.AN
Tương tự \(\Delta\)MAL ~ \(\Delta\)QAN (g.g) thì AL.AQ = AM.AN. Từ đó AK.AP = AL.AQ, dễ có \(\Delta\)LAK ~ \(\Delta\)PAQ (*)
Vì ^XMQ = ^XY'M = ^MLK nên KL // PQ, kết hợp với (*) suy ra (AL,AP) = (AK,AQ) = (KL,PQ) = 0o
Từ đây P,L,A thẳng hàng và Q,K,A thẳng hàng. Khi đó PL.PA = PN.PY'; QK.QA = QX.QN (1)
Mặt khác \(\frac{KM}{NP}=\frac{AK}{AN};\frac{LM}{NQ}=\frac{AL}{AN}\Rightarrow\frac{AK}{AL}=\frac{KM}{NP}.\frac{NQ}{LM}\Rightarrow\frac{QN}{PN}=\frac{AK}{AL}.\frac{LM}{KM}\) (2)
Từ (1) và (2) suy ra \(\frac{QX.QN}{PN.PY'}=\frac{QX}{PY'}.\frac{AK}{AL}.\frac{LM}{KM}=\frac{QK.QA}{PL.PA}\Rightarrow\frac{QX}{PY'}.\frac{LM}{KM}=\frac{AK}{AL}\)
\(\Leftrightarrow\frac{QX}{PY'}=\frac{AK}{AL}.\frac{KM}{LM}\Rightarrow\frac{QX.AM}{PY'.AM}=\frac{AQ.MX}{AP.MY'}\)
Chú ý rằng tứ giác AQXM là tứ giác điều hòa, như vậy PY'.AM = AP.MY'. Suy ra tứ giác APY'M điều hòa
Ta thấy tiếp tuyến tại A của (O1) cắt AM tại C, do đó CY' cũng là tiếp tuyến của (O1)
Lại có CY là tiếp tuyến từ C đến (O1) nên Y trùng Y'. Vậy (MXY) tiếp xúc với BC tại M (đpcm).