\(\sqrt{ 6-\sqrt{11} } -\sqrt{ 6+\sqrt{11} }\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 8 2021
\(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)
L
3
21 tháng 10 2021
\(A=\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}=\dfrac{\sqrt{2}\left(\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}\right)}{\sqrt{2}}=\dfrac{\sqrt{12-2\sqrt{11}}-\sqrt{12+2\sqrt{11}}}{\sqrt{2}}=\dfrac{\sqrt{\left(\sqrt{11}-1\right)^2}-\sqrt{\left(\sqrt{11}+1\right)^2}}{\sqrt{2}}=\dfrac{\sqrt{11}-1-\sqrt{11}-1}{\sqrt{2}}=\dfrac{-2}{\sqrt{2}}=-\sqrt{2}\)
21 tháng 10 2021
\(A=\sqrt{\left(\sqrt{\dfrac{11}{2}}-\sqrt{\dfrac{1}{2}}\right)^2}-\sqrt{\left(\dfrac{11}{2}+\sqrt{\dfrac{1}{2}}\right)^2}\\ A=\sqrt{\dfrac{11}{2}}-\sqrt{\dfrac{1}{2}}-\sqrt{\dfrac{11}{2}}-\sqrt{\dfrac{1}{2}}\\ A=-2\sqrt{\dfrac{1}{2}}=-\dfrac{2\sqrt{2}}{2}=-\sqrt{2}\)
19 tháng 8 2021
Ta có: \(6\sqrt{2}+\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}\)
\(=\dfrac{12+\sqrt{12-2\sqrt{11}}-\sqrt{12+2\sqrt{11}}}{\sqrt{2}}\)
\(=\dfrac{12+\sqrt{11}-1-\sqrt{11}-1}{\sqrt{2}}\)
\(=5\sqrt{2}\)
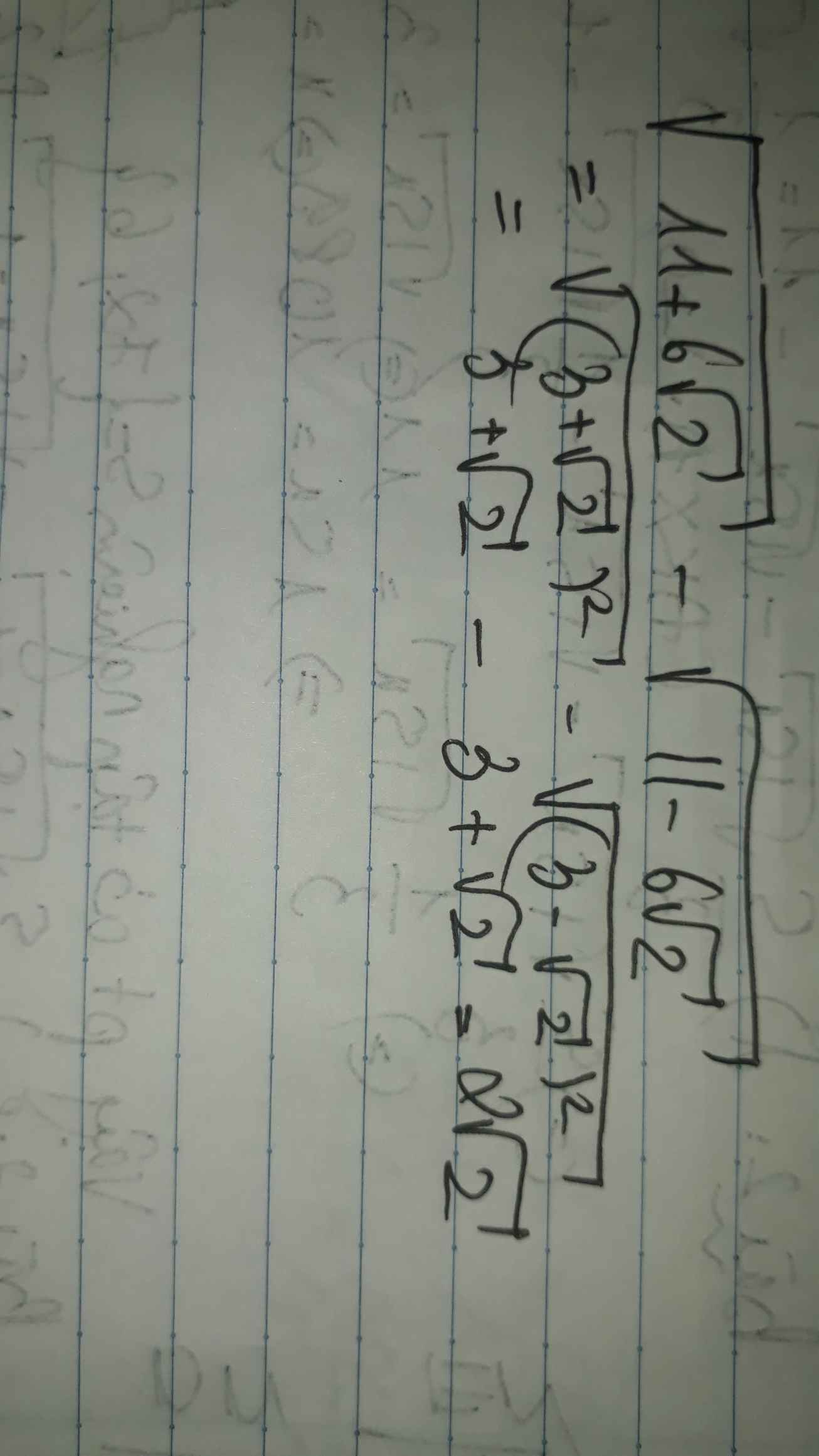
Đặt \(A=\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}\)
\(\Rightarrow A^2=6-\sqrt{11}-2\sqrt{\left(6-\sqrt{11}\right)\left(6+\sqrt{11}\right)}+6+\sqrt{11}\)
\(\Leftrightarrow A^2=12-2\sqrt{36-11}\)
\(\Leftrightarrow A^2=12-2.\sqrt{25}\)
\(\Leftrightarrow A^2=2\)(1)
Vì \(\hept{\begin{cases}\sqrt{6-\sqrt{11}}>0\\\sqrt{6+\sqrt{11}}>0\end{cases}}\)và \(6-\sqrt{11}< 6+\sqrt{11}\)
\(\Rightarrow A=\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}< 0\)(2)
Từ(1),(2) \(\Rightarrow A=-\sqrt{2}\)