Từ 8 chữ số 1,2,,3,,4,6,7,8 lập đươc bao nhiêu số tự nhiên có 8 chữ số khác nhau chia hết cho 1111
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) số nhỏ nhất có tám chữ số khác nhau 12345678 chia cho 1111 được thưong nguyên là 11112.
Quy trình: X=X+1:1111X, CALC X? 11112, ==... Đến khi X=X+1=11115 ta được kết quả so nhỏ nhất cần tìm là 12348765.
b) số lon nhất có tám chữ số khác nhau 87654321 chia cho 1111 được thưong nguyên là 78896.
Quy trình: X=X-1:1111X, CALC X? 78897, ==... Đến khi X=X+1=78894 ta được kết quả so lon nhất cần tìm là 12348765.

Bạn vào xem ở đây nè :http://diendan.hocmai.vn/showthread.php?t=344046

gọi số đó là P=a1a2a3a4a5a6a7a8
P=(a1a2a3a4).10000+(a5a6a7a8) = 9999.(a1a2a3a4)+ (a1a2a3a4) + (a5a6a7a8)
Để P chia hết cho 1111 thì (a1a2a3a4) + (a5a6a7a8) chia hết cho 1111.
Hay 1000.(a1+a5)+ 100.(a2+a6)+ 10.(a3+a7) + (a4+a8) chia hết cho 1111.
-----
Đặt x=a1+a5; y=a2+a6; z=a3+a7; t=a4+a8;
Có 3<= x <= 15
x+y+z+t=36
1000.x+100.y+10.z+t chia hết cho 1111
Thay t= 36-x-y-z. Suy ra 999x+99y+9z+36 chia hết cho 1111.
Mà (9,1111)=1. Suy ra A=111x+11y+z+4 chia hết cho 1111.
A<111.15+11.15+15+4=1849 nên A=1111
+ Nếu x>9 thì A>111.9+11.15+15+4=1183 (vô lý)
+ Nếu x<9, hay x<=8 thì 0< A<111.8+11.15+15+4=1072 <1111 (vô lý)
Vậy x=9.
Suy ra 11.y+z+4=112. Đến đây dễ dàng suy ra x=y=z=t=9.
------
Tìm số bộ thỏa mãn a1+a5=a2+a6=a3+a7=a4+a8=9
Ta phải chọn (a1,a5) (a2,a6) (a3,a7) (a4,a8) vào các bộ (1,8) (2,7) (3,6) (4,5)
Có 4.3.2.1 cách chọn như vậy
Ứng với mỗi cách chọn lại có thể hoán vị như sau: (1,8) thành (8,1);(2,7) thành (7,2);(3,6) thành (6,3); (4,5) thành (5,4). => Có 2^4 cách
Tóm lại số số thỏa mãn là 4.3.2.1.2^4=384

Đáp án D

Do X có 8 phần tử và tổng các phần tử là 36 nên A chia hết cho 9, lại có (9;11) = 1 nên A chia hết cho 9999.
Ta có:
![]()
![]()
![]()
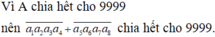
![]()
![]()
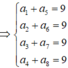
Có 8 cách chọn a 1 . Với mỗi a 1 sẽ cho 1 cách chọn cho duy nhất cho a 5
Có 8 cách chọn a 2 . Với mỗi a 1 sẽ cho 1 cách chọn cho duy nhất cho a 6
Có 8 cách chọn a 3 . Với mỗi a 1 sẽ cho 1 cách chọn cho duy nhất cho a 7
Có 8 cách chọn a 4 . Với mỗi a 1 sẽ cho 1 cách chọn cho duy nhất cho a 8
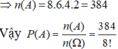

Chọn C
+ Gọi số cần tìm là ![]()
Ta có tổng các chữ số của A là 1 + 2 + 3 + 4 + .... + 8 = 36 chia hết cho 9 nên A chia hết cho 9.
Do 9 và 111 có ƯCLN là nên A chia hết cho 9999.
Đặt ![]() Ta có:
Ta có:
![]() chia hết cho 9999 => x + y chia hết cho 9999
chia hết cho 9999 => x + y chia hết cho 9999
Mà ![]()
![]()
![]()
![]()
![]()
![]()
![]()
+ Từ tập X có 4 cặp số ![]() nên có: 8 cách chọn
a
1
; 6 cách chọn
a
2
; 4 cách chọn
a
3
và 2 cách chọn
a
4
.
nên có: 8 cách chọn
a
1
; 6 cách chọn
a
2
; 4 cách chọn
a
3
và 2 cách chọn
a
4
.
Vì a i và b i tạo thành một cặp để a i + b i = 9 nên chọn a i có luôn b i .
=> Số các số cần tìm là: 8.6.4.2 = 384 số
Vậy xác suất cần tìm là:
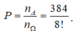

Èo toàn bài khó nhằn :( Thôi làm được mỗi câu 2, câu 1 thì...dẹp đi
\(n\left(\Omega\right)=9.9.8.7.6.5\)
Số lẻ vậy thì f={1;3;5;7;9}
Nhưng nếu f=1 thì ko tồn tại a thỏa mãn a<f do a khác 0
f=3 cũng ko thỏa mãn do nếu a=1; b=2; nhưng ko tồn tại c thỏa mãn :v
f=5 tương tự, ko tồn tại e thỏa mãn
=> f={7;9}
Nếu f=7 thì (a,b,c,d,e)={1;2;3;4;5;6} và chỉ có duy nhất 1 cách sắp xếp \(\Rightarrow C^5_6\left(cach\right)\)
Nếu f=9 thì (a,b,c,d,e)={1;2;3;4;5;6;7;8} và chỉ có duy nhất một cách xếp \(\Rightarrow C^5_8\left(cach\right)\)
\(\Rightarrow n\left(A\right)=C^5_6+C^5_8\) \(\Rightarrow p\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)
Gọi A là số tự nhiên có 8 chữ số a1a2a3a4a5a6a7a8 chia hết cho 1111
9999a1a2a3a4 + a1a2a3a4+a5a6a7a8 để A chia hết cho 1111 thì a1a2a3a4+a5a6a7a8 chia hết cho 1111
1000(a1 + a5) + 100(a2 + a6) + 10(a3 + a7) + (a4+ a8) (1) chia hết cho 1111
đặt (a1 + a5) = x
(a2 + a6) = y
(a3 + a7) = z
(a4+ a8) = t
3<=x<=15
xét đk
suy ra x = 9
suy ra x=y=z=t= 9
suy ra x+y+z+t=36 suy ra t= 36-x-y-z
thế vào (1) suy ra
999(a1 + a5) + 99(a2 + a6) + 9(a3 + a7) =36
hoán vị .......
suy ra có 3840 số