Cho hình bình hành ABCD với góc BAD <90 độ.Đường phân giác của góc BCD cắt đường tròn ngoại tiếp tam giác BCD tại O khác C. Kẻ đường thẳng d qua A và vuông góc vói OC. Đường thẳng d làn lượ cắt các đường thẳng CB,CD tại E,F.
a)Chứng minh rằng \(\Delta OBE=\Delta ODC\)
b)Chúng minh rằng O là tâm đường tròn ngoại tiếp tam giác CEF.
c)Gọi giao điểm của OC và BD là I,chứng minh rằng IB.BE.EI=ID.DF.FI.


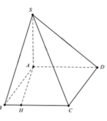
a) Ta thấy \(\Delta\)CEF có CO vừa là phân giác ^ECF, vừa vuông góc với EF, suy ra \(\Delta\)CEF cân tại C
Vì tứ giác ABCD là hình bình hành nên DC = AB = BE (1)
Ta có ^BCO = ^DCO suy ra (OB = (OD hay OB = OD (2); lại có ^ODC = ^OBE (Tứ giác BCDO nội tiếp) (3)
Từ (1);(2);(3) suy ra \(\Delta\)OBE = \(\Delta\)ODC (c.g.c) (đpcm).
b) Từ câu a ta có OC = OE. Tương tự OC = OF. Vậy O là tâm ngoại tiếp \(\Delta\)CEF (đpcm).
c) Dễ có \(\Delta\)OIB ~ \(\Delta\)DIC suy ra IB.DC = IC.OB hay IB.BE = IC.OB. Tương tự ID.DF = IC.OD
Từ đó IB.BE = ID.DF (Vì OB = OD). Mà EI = FI (Vì I thuộc trung trực EF) nên IB.BE.EI = ID.DF.FI (đpcm).