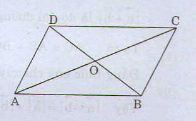
a. Cho hình bình hành ABCD có tâm O. Chứng minh rằng: \(\overrightarrow{DA}\) - \(\overrightarrow{DB}\) = \(\overrightarrow{OD}\) - \(\overrightarrow{OC}\)
b. Cho AK và BM là 2 đường trung tuyến của tam giác ABC.
Hãy phân tích các vectơ \(\overrightarrow{AC}\) ; \(\overrightarrow{AB}\) theo 2 vectơ u = \(\overrightarrow{AK}\) ; v = \(\overrightarrow{BM}\)
Giúp mình giải bài này nha! ⚡KN⚡ Cảm Ơn Mọi Người!❤


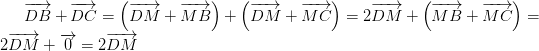
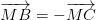
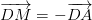
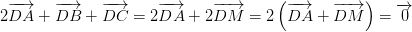
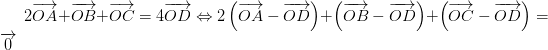
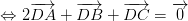 luôn đúng theo câu a
luôn đúng theo câu a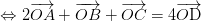 , với O là điểm tùy ý
, với O là điểm tùy ý
a/ \(\overrightarrow{DA}-\overrightarrow{DB}=\overrightarrow{DA}+\overrightarrow{BD}=\overrightarrow{BA}\)
\(\overrightarrow{OD}-\overrightarrow{OC}=\overrightarrow{OD}+\overrightarrow{CO}=\overrightarrow{CD}\)
Mà \(\overrightarrow{BA}=\overrightarrow{CD}\) (t/c hình bình hành) \(\Rightarrow\) đpcm
b/ Theo tính chất trung tuyến:
\(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\\\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AC}+\overrightarrow{BC}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\Rightarrow\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{AC}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\Rightarrow2\overrightarrow{AC}-\overrightarrow{AB}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\\2\overrightarrow{AC}-\overrightarrow{AB}=2\overrightarrow{AK}+2\overrightarrow{BM}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\frac{4}{3}\overrightarrow{AK}+\frac{2}{3}\overrightarrow{BM}\\\overrightarrow{AB}=\frac{2}{3}\overrightarrow{AK}-\frac{2}{3}\overrightarrow{BM}\end{matrix}\right.\)