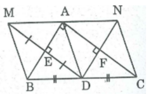
Cho tam giác ABC cân tại A. Gọi M,N,P là trung điểm của BC, AC, AB. E đối xứng với P qua N, F đối xứng với N qua BC
a, CM: ANFM là hbh
b, Đường thẳng ME gao AB tại K. Chứng minh K đối xứng với P qua B
c, Cm: E,C,F thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 2 2022
a: Xét tứ giác AKMN có
MN//AK
AN//MK
Do đó: AKMN là hình bình hành
mà \(\widehat{NAK}=90^0\)
nên AKMN là hình chữ nhật
b: Xét ΔAMQ có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔAMQ cân tại A
mà AN là đường cao
nên AN là tia phân giác của góc MAQ(1)
Xét ΔAME có
AK là đường cao
AK là đường trung tuyến
DO đó: ΔAME cân tại A
mà AK là đường cao
nên AK là tia phân giác của góc MAE(2)
Từ (1) và (2) suy ra \(\widehat{QAE}=2\cdot\left(\widehat{MAN}+\widehat{MAK}\right)=2\cdot90^0=180^0\)
hay Q,E,A thẳng hàng
7 tháng 1 2023
a: E đối xứng M qua AB
nên AB là trung trực của ME
=>AB vuông góc với ME tại trung điểm của ME
=>AB là phân giác của góc EAM(1)
E đối xứng N qua AC
nên AC là trung trực của NE
=>AC vuông góc với NE tại trung điểm của NE
=>AC là phân giác của góc EAN(2)
Xét tứ giác AIEK có
góc AIE=góc AKE=góc KAI=90 độ
nên AIEK làhình chữ nhật
b: Từ (1), (2) suy ra góc NAM=2*90=180 độ
=>N,A,M thẳng hàng
mà AM=AN
nên A là trung điểm của MN
CM
19 tháng 1 2017
Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng qua điểm A.
5 tháng 1 2023
a: Xét tứ giác APBI có
M là trung điểm chung của AB và PI
AB vuông góc với PI
Do đó: APBI là hình thoi
b: Xét tứ giác AMPH có
góc AMP=góc AHP=góc MAH=90 độ
nên AMPH là hình chữ nhật
c: Xét ΔAPK có
AC vừa là đường cao, vừa là trung tuyến
nên ΔAPK cân tại A
=>AC là phân giác của góc KAP(1)
APBI là hình thoi
nên AB là phân giác của góc IAP(2)
Từ (1), (2) suy ra góc KAI=2*90=180 độ
=>K,A,I thẳng hàng
