Cho tam giác ABC vuông cân tại A. M thuộc BC. D,E là chân dduongf vuông góc kẻ từ M đến AB<AC>
a, CM: AM=ED
b, TÍnh chu vi tứ giác ADME nếu AC=6cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 5 2017
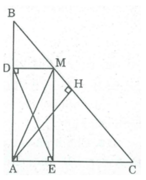
Xét tứ giác ADME, ta có:
∠ A= 90 0 (gt)
MD ⊥ AB (gt)
⇒ ∠ (ADM) = 90 0
Lại có, MD ⊥ AC ⇒ ∠ (MEA) = 90 0
Suy ra tứ giác ADME là hình chữ nhật (vì có 3 góc vuông)
∆ ABC vuông cân tại A ⇒ ∠ B = 45 0 và AB = AC = 4cm
Suy ra: ∆ DBM vuông cân tại D
⇒ DM = DB
Chu vi hình chữ nhật ADME bằng:
2(AD + DM) = 2(AD + DB) = 2AB = 2.4 = 8 (cm)
TD
6 tháng 12 2015
các bước nè
C/m tam giác DBM vuông cân tại D =>DB=DM
=>AD+DB=4cm=AD+DM
=>chu vi hcn ADME là (AD+DM)*2=4*2=8cm
bạn xem thử nhé ^_^
BB
8 tháng 11 2017
MDA = DAE = AEM = 90
=> ADME là hcn
Tam giác ABC vuông cân tại A
=> ACB = ABC = 45
mà MEC = 90
=> Tam giác EMC vuông cân tại E
=> EM = EC
mà DM = AE (ADME là hcn)
=> EM + DM = EC + AE = AC = 4 (cm)
PADME = 2 . (EM + DM) = 2 . 4 = 8 (cm)
DE = AM (ADME là hcn)
=> DE nhỏ nhất
<=> AM nhỏ nhất
<=> AM _I_ BC tại M
mà tam giác ABC vuông cân tại A
=> AM là đường trung tuyến
=> M là trung điểm
Vậy DE nhỏ nhất <=> M là trung điểm của BC.
a.Xét tứ giác ADME có \(\widehat{A}=\widehat{E}=\widehat{D}=90^o\) = > tứ giác ADME là HCN
=> AM= DE ( do AM, DE là 2 đường chéo ) (đpcm)
b. Xét tam giác MEC có \(\widehat{E}-90^o\Rightarrow\widehat{EMC}+\widehat{C}=90^o\)
\(\Rightarrow\widehat{EMC}=90^o-45^o=45^o\)
=> tam giác MEC cân tại E
=> ME=EC
Ta có: \(C_{ADME}=2.\left(AE+ME\right)=2.\left(AE+EC\right)=2.AC=2.6=12\left(cm\right)\)
Vậy chu vi tứ giác ADME là 12 cm