Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai chân cổng bằng 162m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất, người ta thả một sợi dây chạm đất ( dây căng thẳng theo phương vuông góc với đất ). Vị trí chạm đất của đầu sợi dây này cách chân cổng một đoạn 10m. Giả sử số liệu trên là chính xác. Hãy tính độ cao của cổng Arch ( tính từ mặt đất đến điểm cao nhất của cổng )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan



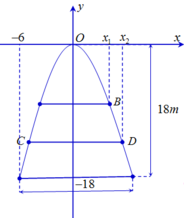
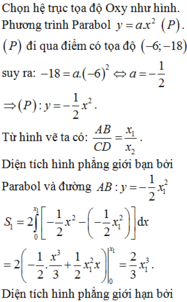
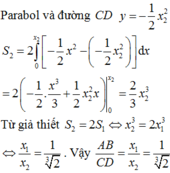
Đặt hệ trục tọa độ Oxy vào cổng với gốc tọa độ trùng điểm chính giữa hai chân cổng
Gọi 2 chân cổng là A và B, điểm cao nhất là C, điểm có độ cao 43m là D
\(\Rightarrow A\left(-81;0\right)\) ; \(B\left(81;0\right)\); \(D\left(71;43\right)\)
Phương trình parabol có dạng \(y=ax^2+bx+c\)
Thay tọa độ A; B; C vào ta được hệ:
\(\left\{{}\begin{matrix}81^2.a-81b+c=0\\81^2a+81b+c=0\\71^2a+71b+c=43\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\frac{43}{1520}\\b=0\\c=\frac{81^2.43}{1520}\end{matrix}\right.\)
\(\Rightarrow\) Độ cao cổng cũng là tung độ đỉnh C
\(\Rightarrow h=y_C=c\simeq185,6\left(m\right)\)
D tại sao lại là 71 mà k phải là - 71 á bạn?