Phương trình đối xứng với sinx và cosx
2cos2x + (sinxcosx-1) (sinx + cosx) = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
22 tháng 10 2019
1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0 ( 1 ) T a c ó : 1 - sin 2 x = sin x - cos x 2 ⇔ 2 cos 2 x = 2 ( cos 2 x - sin 2 x ) = - 2 ( sin x - cos x ) ( sin x + cos x ) V ậ y ( 1 ) ⇔ ( sin x - cos x ) ( 1 + sin x - cos x - 2 sin x - 2 cos x ) = 0 ⇔ ( sin x - cos x ) ( 1 - sin x - 3 cos x ) = 0
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
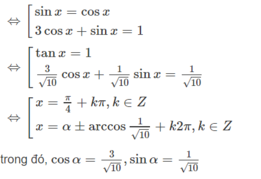
2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 10 2020
1.
Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{t^2-1}{2}\end{matrix}\right.\)
Pt trở thành:
\(t^3+\frac{t^2-1}{2}-1=0\)
\(\Leftrightarrow2t^3+t^2-3=0\)
\(\Leftrightarrow\left(t-1\right)\left(2t^2+3t+3\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 10 2020
4.
Đặt \(sinx-cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{1-t^2}{2}\end{matrix}\right.\)
Pt trở thành:
\(t^3=1+\frac{1-t^2}{2}\)
\(\Leftrightarrow2t^3+t^2-3=0\)
\(\Leftrightarrow\left(t-1\right)\left(2t^2+3t+3\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow...\)
CM
3 tháng 8 2018
Đáp án C
Nhận thấy cos x = 0 không phải là nghiệm của phương trình. Chia cả hai vế của phương trình cho cosx ta được
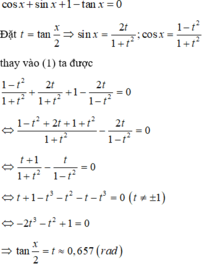
Vậy có 1 điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác.
CM
5 tháng 8 2019
Đáp án C
Nhận thấy cosx = 0 không phải là nghiệm của phương trình. Chia cả hai vế của phương trình cho cosx ta được
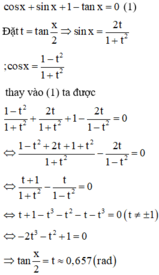
Vậy có 1 điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác.
\(\Leftrightarrow2\left(cos^2x-sin^2x\right)+\left(sinx.cosx-1\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2\left(cosx-sinx\right)+sinx.cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\\2\left(cosx-sinx\right)+sinx.cosx-1=0\end{matrix}\right.\)
TH1: \(sinx+cosx=0\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=0\)
\(\Rightarrow x=-\frac{\pi}{4}+k\pi\)
TH2: \(2\left(cosx-sinx\right)+sinx.cosx-1=0\)
Đặt \(cosx-sinx=-\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=a\) (\(\left|a\right|\le\sqrt{2}\))
\(\Rightarrow a^2=1-2sinx.cosx\Rightarrow sinx.cosx=\frac{1-a^2}{2}\)
\(2a+\frac{1-a^2}{2}-1=0\)
\(\Leftrightarrow a^2-4a+1=0\Rightarrow\left[{}\begin{matrix}a=2+\sqrt{3}\left(l\right)\\a=2-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow-\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=2-\sqrt{3}\)
\(\Rightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{3}-2}{\sqrt{2}}=sin\alpha\)
\(\Rightarrow...\)
Nghiệm thứ 2 xấu vậy, bạn có ghi đề nhầm chỗ nào ko nhỉ?