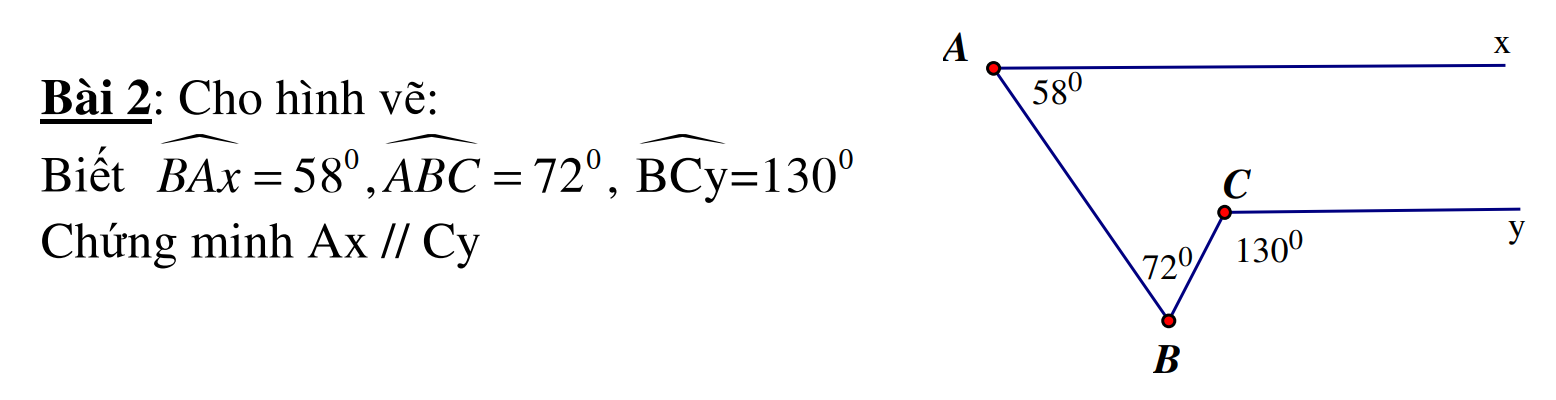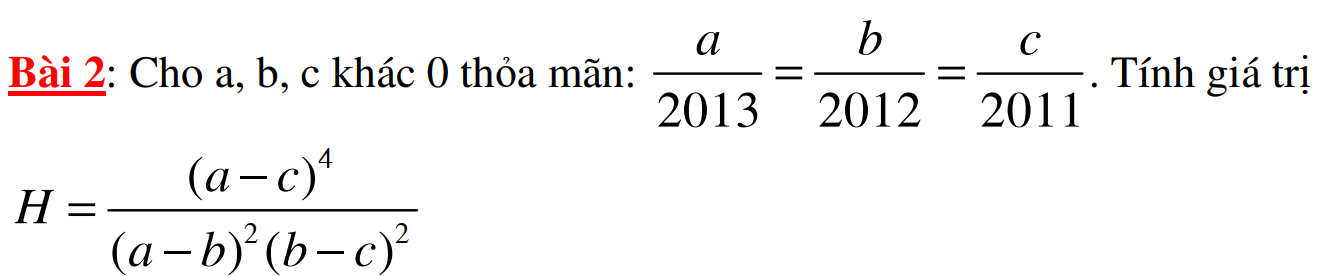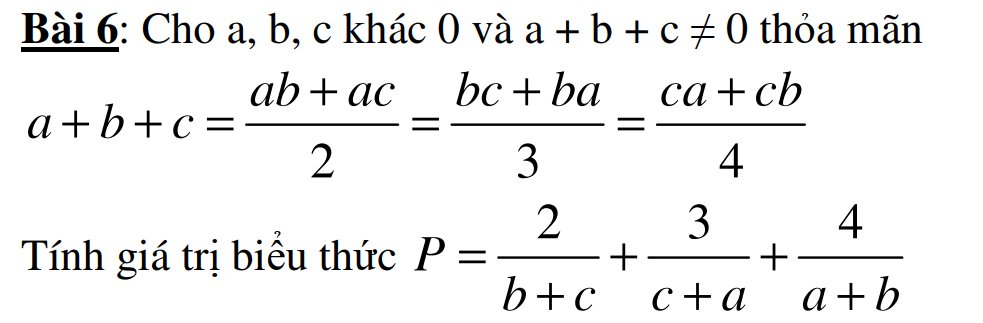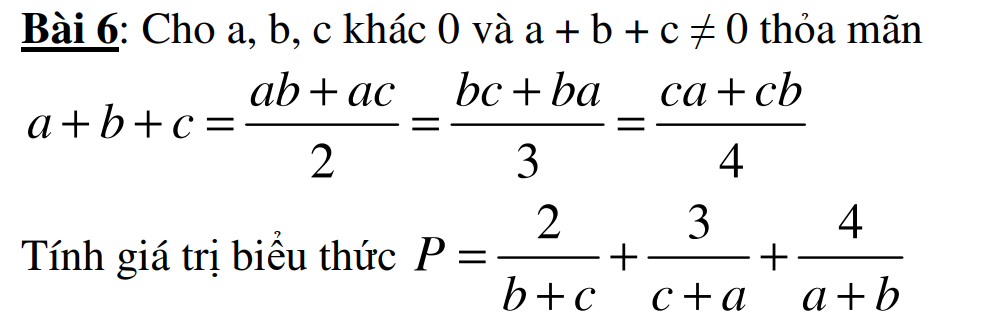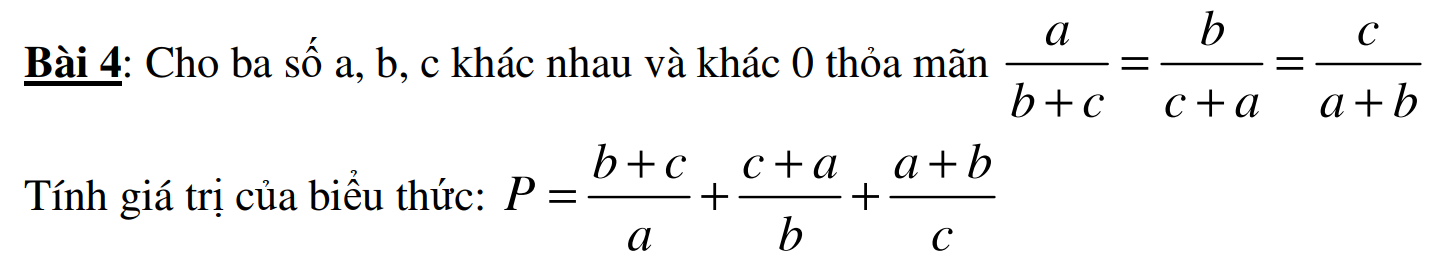Ai làm giúp...
Đọc tiếp
Ai làm giúp vớiiiiiiiiiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 11 2021
\(\Rightarrow2x-1=\dfrac{2}{5}\Rightarrow2x=\dfrac{7}{5}\Rightarrow x=\dfrac{7}{10}\left(D\right)\)
V
22 tháng 7 2021
a. \(A=\left(4-5x\right)^2-\left(3+5x\right)^2\\ =\left(4-5x+3+5x\right)\left(4-5x-3-5x\right)\\ =7.\left(-5x\right)=-35x\)
b. \(B=\left(3x-1\right)\left(1+3x\right)-\left(3x+1\right)^2\\ =9x^2-1-\left(9x^2+6x+1\right)\\ =9x^2-1-9x^2-6x-1\\ =-6x-2\)
22 tháng 7 2021
a) Ta có: \(A=\left(4-5x\right)^2-\left(5x+3\right)^2\)
\(=\left(4-5x-5x-3\right)\left(4-5x+5x+3\right)\)
\(=7\left(-10x+1\right)\)
\(=-70x+7\)
b) Ta có: \(B=\left(3x-1\right)\left(3x+1\right)-\left(3x+1\right)^2\)
\(=\left(3x+1\right)\left(3x-1-3x-1\right)\)
\(=-2\left(3x+1\right)\)
\(=-6x-2\)
c) Ta có: \(C=\left(2x+5\right)^3-\left(2x-5\right)^3-\left(120x^2+49\right)\)
\(=8x^3+60x^2+150x+125-\left(8x^3-60x^2+150x-125\right)-120x^2-49\)
\(=8x^3-60x^2+150x+76-8x^3+60x^2-150x+125\)
\(=201\)
TT
1
12 tháng 8 2021
từ điểm B kẻ \(Bz//Cy=>\angle\left(BCy\right)+\angle\left(CBz\right)=180^o\)(góc trong cùng phía)
\(=>\angle\left(CBz\right)=180^o-130^o=50^o\)
\(=>\angle\left(ABz\right)=\angle\left(ABC\right)+\angle\left(CBz\right)=50^o+72^o=122^o\)
\(=>\angle\left(BAx\right)+\angle\left(ABz\right)=180^o\)
mà 2 góc này ở vị trí trong cùng phía
\(=>Ax//Bz=>Ax//Cy\)
NK
1
15 tháng 9 2021
Áp dụng t/c dãy tỉ số bằng nhau
\(\dfrac{a}{2013}=\dfrac{b}{2012}=\dfrac{c}{2011}=\dfrac{a-c}{2}=\dfrac{a-b}{1}=\dfrac{b-c}{1}\\ \Rightarrow a-c=2\left(a-b\right)=2\left(b-c\right)\)
\(\Rightarrow H=\dfrac{\left[2\left(a-b\right)\right]^4}{\left(a-b\right)^2\left(a-b\right)^2}=\dfrac{16\left(a-b\right)^4}{\left(a-b\right)^4}=16\)
NK
0
NK
0
NK
2
15 tháng 9 2021
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{2\left(a+b+c\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}b+c=2a\\c+a=2b\\a+b=2c\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{2a}{a}+\dfrac{2b}{b}+\dfrac{2c}{c}=2+2+2=6\)
S
15 tháng 9 2021
P=
\(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{a}{b+c}.\left(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\right):\left(\dfrac{a}{b+c}\right)=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{a}{b+c}+\dfrac{a+b}{c}.\dfrac{a}{b+c}\right):\dfrac{a}{b+c}=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{b}{c+a}+\dfrac{a+b}{c}.\dfrac{c}{a+b}\right):\dfrac{a}{b+c}=\left(1+1+1\right):\dfrac{a}{b+c}=3.\dfrac{b+c}{a}=\dfrac{3b+3c}{a}\)
