Chứng minh rằng n3+3n2+ 2n chia hết cho 6 với mọi n ϵ Z
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
LH
2
AH
Akai Haruma
Giáo viên
19 tháng 10 2019
Lời giải:
* CM $A$ chia hết cho $2$
Ta thấy $(7n+1)-n=6n+1$ lẻ, chứng tỏ $7n+1,n$ luôn khác tính chẵn lẻ.
Do đó luôn tồn tại 1 trong 2 số là chẵn
$\Rightarrow A=n(2n+1)(7n+1)$ chẵn, hay $A\vdots 2(*)$
* CM $A$ chia hết cho $3$. Xét modulo $3$ cho $n$:
Nếu $n=3k(k\in\mathbb{Z}$
$\Rightarrow n\vdots 3\Rightarow A=n(2n+1)(7n+1)\vdots 3$
Nếu $n=3k+1\Rightarrow 2n+1=2(3k+1)+1=3(2k+1)\vdots 3$
$\Rightarrow A=n(2n+1)(7n+1)\vdots 3$
Nếu $n=3k+2\Rightarrow 7n+1=7(3k+2)+1=3(7k+5)\vdots 3$
$\Rightarrow A=n(2n+1)(7n+1)\vdots 3$
Vậy tóm lại $A\vdots 3(**)$
Từ $(*); (**), mà $(2,3)=1$ nên $A\vdots (2.3)$ hay $A\vdots 6$ (đpcm)
AH
Akai Haruma
Giáo viên
3 tháng 10 2019
Lời giải:
* CM $A$ chia hết cho $2$
Ta thấy $(7n+1)-n=6n+1$ lẻ, chứng tỏ $7n+1,n$ luôn khác tính chẵn lẻ.
Do đó luôn tồn tại 1 trong 2 số là chẵn
$\Rightarrow A=n(2n+1)(7n+1)$ chẵn, hay $A\vdots 2(*)$
* CM $A$ chia hết cho $3$. Xét modulo $3$ cho $n$:
Nếu $n=3k(k\in\mathbb{Z}$
$\Rightarrow n\vdots 3\Rightarow A=n(2n+1)(7n+1)\vdots 3$
Nếu $n=3k+1\Rightarrow 2n+1=2(3k+1)+1=3(2k+1)\vdots 3$
$\Rightarrow A=n(2n+1)(7n+1)\vdots 3$
Nếu $n=3k+2\Rightarrow 7n+1=7(3k+2)+1=3(7k+5)\vdots 3$
$\Rightarrow A=n(2n+1)(7n+1)\vdots 3$
Vậy tóm lại $A\vdots 3(**)$
Từ $(*); (**), mà $(2,3)=1$ nên $A\vdots (2.3)$ hay $A\vdots 6$ (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2021
a.
Đề bài sai, ví dụ \(n=1\) lẻ nhưng \(1^2+4.1+8=13\) ko chia hết cho 8
b.
n lẻ \(\Rightarrow n=2k+1\)
\(n^3+3n^2-n-3=n^2\left(n+3\right)-\left(n+3\right)=\left(n^2-1\right)\left(n+3\right)=\left(n-1\right)\left(n+1\right)\left(n+3\right)\)
\(=\left(2k+1-1\right)\left(2k+1+1\right)\left(2k+1+3\right)\)
\(=8k\left(k+1\right)\left(k+2\right)\)
Do \(k\left(k+1\right)\left(k+2\right)\) là tích 3 số tự nhiên liên tiếp nên chia hết cho 6
\(\Rightarrow8k\left(k+1\right)\left(k+2\right)\) chia hết cho 48
2 tháng 2 2023
A=n^3+3n^2+5n+3
<=>A=n^3+n^2+2n^2+2n+3n+3
<=>A=(n^2+2n+3)(n+1)
<=>A=n(n+1)(n+2)+3(n+1)
Ta thấy, n(n+1)(n+2) là tích ba số nguyên liên tiếp nên n(n+1)(n+2) chia hết cho 6 hay n(n+1)(n+2) chia hết cho 3(1)
Mặt khác, 3(n+1) luôn chia hết cho 3 với mọi x là số nguyên(2)
Từ (1) và (2)
=>n(n+1)(n+2)+3(n+1) chia hết cho 3
2 tháng 2 2023
Đặt B=n^3+3n^2+5n
Khi n=1 thì B=1+3+5=9 chia hết cho 3
Khi n>1 thì Giả sử B=n^3+3n^2+5n chiahết cho 3
Ta cần chứng minh (n+1)^3+3(n+1)^2+5(n+1)chia hết cho 3
=n^3+3n^2+3n+1+3n^2+6n+3+5n+5
=n^3+3n^2+5n+3n^2+9n+9 chia hêt cho 3
=>B chia hết cho 3
=>A chia hết cho 3
PT
1
CM
16 tháng 4 2018
Cách 1: Quy nạp
Đặt An = n3 + 3n2 + 5n
+ Ta có: với n = 1
A1 = 1 + 3 + 5 = 9 chia hết 3
+ giả sử với n = k ≥ 1 ta có:
Ak = (k3 + 3k2 + 5k) chia hết 3 (giả thiết quy nạp)
Ta chứng minh Ak + 1 chia hết 3
Thật vậy, ta có:
Ak + 1 = (k + 1)3 + 3(k + 1)2 + 5(k + 1)
= k3 + 3k2 + 3k + 1 + 3k2 + 6k + 3 + 5k + 5
= (k3 + 3k2 + 5k) + 3k2 + 9k + 9
Theo giả thiết quy nạp: k3 + 3k2 + 5k ⋮ 3
Mà 3k2 + 9k + 9 = 3.(k2 + 3k + 3) ⋮ 3
⇒ Ak + 1 ⋮ 3.
Cách 2: Chứng minh trực tiếp.
Có: n3 + 3n2 + 5n
= n.(n2 + 3n + 5)
= n.(n2 + 3n + 2 + 3)
= n.(n2 + 3n + 2) + 3n
= n.(n + 1)(n + 2) + 3n.
Mà: n(n + 1)(n + 2) ⋮ 3 (tích của ba số tự nhiên liên tiếp)
3n ⋮ 3
⇒ n3 + 3n2 + 5n = n(n + 1)(n + 2) + 3n ⋮ 3.
Vậy n3 + 3n2 + 5n chia hết cho 3 với mọi ∀n ∈ N*
TV
0
PT
1
LH
1
19 tháng 10 2019
Ta có :
\(n^3-13n=n^3-n-12n=n\left(n^2-1\right)-12n=n\left(n-1\right)\left(n+1\right)-12n\)
Với mọi số nguyên n ta có :
+) \(n\left(n-1\right)\left(n+1\right)⋮6\) (tích của 3 số nguyên liên tiếp )
+) \(12n⋮6\)
\(\Leftrightarrow n\left(n-1\right)\left(n+1\right)-12n⋮6\)
\(\Leftrightarrow n^3-12n⋮6\left(đpcm\right)\)
14 tháng 8 2015
a) Ta có: m^3-m = m(m^2-1^2) = m.(m+1)(m-1) là tích của 3 số nguyên liên tiếp
=> m(m+1)(m-1) chia hết cho 3 và 2
Mà (3,2) = 1
=> m(m+1)(m-1) chia hết cho 6
=> m^3 - m chia hết cho 6 V m thuộc Z
b) Ta có: (2n-1)-2n+1 = 2n-1-2n+1 = 0-1+1 = 0 luôn chia hết cho 8
=> (2n-1)-2n+1 luôn chia hết cho 8 V n thuộc Z
Tick nha pham thuy trang
14 tháng 8 2015
a, m3 - m = m( m2 - 12) = m(m - 1 ) ( m + 1) => 3 số nguyên liên tiếp : hết cho 6
mk chỉ biết có thế thôi
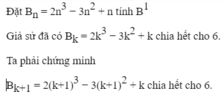
\(n^3+3n^2+2n=n\left(n^2+3n+2\right)=n\left(n+1\right)\left(n+2\right)⋮6\) (vì là 3 số nguyên lt)
\(n^3+3n^2+2n-n\left(n^2+3n+2\right)\)
\(=n\left[n\left(n+1\right)+2\left(n+1\right)\right]=n\left(n+1\right)\left(n+2\right)\)
Là tích 3 số nguyên liên tiếp nên có một số chia hết cho 2 và một số chia hết cho 3
\(\Rightarrow n^3+3n^2+2n=n\left(n+1\right)\left(n+2\right)⋮2.3=6\forall n\in Z\)