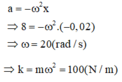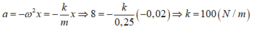Một con lắc lò xo gồm quả cầu m=100(g), lò xo k = 40N/m, dao động điều hòa theo phương nằm ngang trên trục Ox, gốc toạ độ O ở vị trí cân bằng. Biết lúc t = 0 vật có li độ x = +cm và có vận tốc v= +80(cm/s). Phương trình dao động của quả cầu là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Phương pháp: Sử dụng công thức tính gia tốc trong dao động điều hòa của con lắc lò xo
Cách giải:
Ta có:
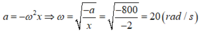
=> Độ cứng k = mω2 = 0,25.202 = 100 N/m
=> Chọn D

Chọn C
+ ω = 2π : T = 20 rad/s.
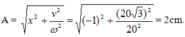
+ t = 0: x = 2cosφ = -1 => 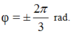
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.

Câu này dễ mà bạn, áp dụng CT liên hệ giữa gia tốc với li độ.
\(a=-\omega^2.x\Rightarrow \omega=\sqrt{\dfrac{-a}{x}}=20(rad/s)\)
\(\Rightarrow k=m.\omega^2=0,25.20^2=100(N/m)\)

Đáp án C
Cơ năng của con lắc lò xo được xác định bởi biểu thức

T = 0,63s ⇒ ω = 10
Tại t = 0 vật ở biên dương nên phương trình dao động của vật là
x = 10cos10t (cm)

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)