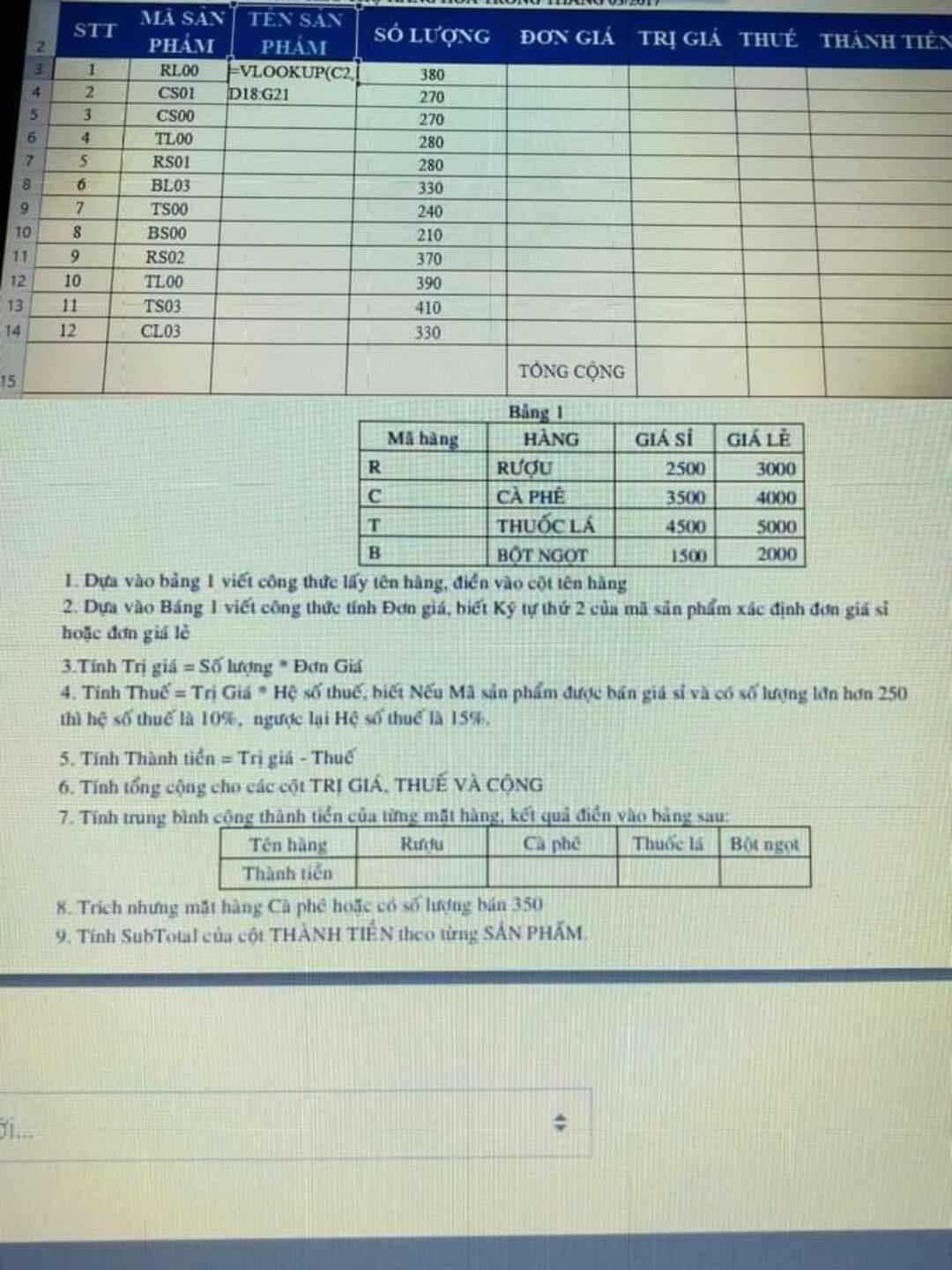
Giúp mình với ạ không cần làm hết đâu!! :33
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
J
mng giúp mình với ạ, mng làm bnh thì mng làm ạ, kh cần làm hết đâu ạ
1
14 tháng 2 2022
Bài 6:
a: Trên tia Ox, ta có: OA<OB
nên điểm A nằm giữa hai điểm O và B
=>OA+AB=OB
hay AB=3cm
b: Trên tia Ax, ta có: AB<AC
nên điểm B nằm giữa hai điểm A và C
mà AB=AC/2
nên B là trung điểm của AC
K
13 tháng 12 2020
11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
K
13 tháng 12 2020
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)
NQ
0
KA
1
21 tháng 10 2021
Bài 3:
1: Ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+2}{x-4}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
12 tháng 1 2022
1: \(\Leftrightarrow x-2-7x+7=-1\)
=>-6x+5=-1
hay x=1(loại)
3: \(\Leftrightarrow\left(x+2\right)\left(x-1\right)-\left(x+1\right)\left(x+3\right)=4\)
\(\Leftrightarrow x^2+x-2-x^2-4x-3=4\)
=>-3x=9
hay x=-3(loại)
4: \(\Leftrightarrow x^2+2x+1-x^2+2x-1=3x\cdot\dfrac{x+1-x+1}{x+1}\)
\(\Leftrightarrow4x=\dfrac{6x}{x+1}\)
\(\Leftrightarrow4x^2+4x-6x=0\)
\(\Leftrightarrow4x^2-2x=0\)
=>2x(2x-1)=0
hay \(x\in\left\{0;\dfrac{1}{2}\right\}\)
Bài 1:
a: \(A\cap B=\left(-\infty;4\right)\)