Cho O, H, G lần lượt là trọng tâm của đường tròn ngoại tiếp, trực tâm, trọng tâm của tam giác ABC.
a/ CM O, H, G cùng nằm trên một đường thẳng
b/GH= 2 GO
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 4 2016
Cho tam giác ABC có trực tâm H , trọng tâm G , O là tâm đường tròn
ngoại tiếp , I là trung điểm BC , AD là đường kính của (O) .
Chứng minh H , G , O thẳng hàng ?
Giải :
Ta có : góc DCA = góc DBA = 90 độ ( góc nội tiếp chắn 1/2 (O))
Xét tứ giác BHCD ta có :
BH // DC ( vì cùng vuông góc với AC )
CH // DB ( vì cùng vuông góc với AB )
Do đó tứ giác BHCD là hình bình hành .
===> H , I , D thẳng hàng và IH = ID (t/c đường chéo hbhành)
Ta lại có : OI = 1/2 AH ( đ.trung bình tam giác DAH ) (1)
GI = 1/2 GA (t/chất trọng tâm của ABC ) (2)
góc HAG = góc GIO ( so le trong vì AH // OI ) (3)
Do đó tam giác GAH đồng dạng tam giác GIO ( c.g.c)
===> góc HGA = góc IGO (góc tương ứng của 2 t.giác đ.dạng )
Vì góc HGA và góc IGO là 2 góc ở vị trí đối đỉnh bằng nhau nên ta suy ra H , G , O thẳng hàng .
Vậy trong 1 tam giác trực tâm , trọng tâm , tâm đường tròn ngoại tiếp cùng nằm trên 1 đường thẳng đó là đường thẳng Euler !
20 tháng 2 2019
Nguyễn Thị Hội là con nào????????????????????????????????????????????????????????????????????????????????????????
20 tháng 2 2019
) Gọi M là trung điểm BC. Lấy điểm D sao cho O là trung điểm CD
Xét Δ BCD có M là trung điểm BC, O là trung điểm CD \Rightarrow OM là đường trung bình của Δ BCD
\Rightarrow OM=12DB và OM // DB
mà OM⊥BC ( OM là đường trung trực của BC ) \Rightarrow DB⊥BC
mà AH⊥BC( AH là đường cao của ΔABC ) \Rightarrow AH // DB
Xét ΔABH và ΔBAD có
HABˆ=DBAˆ( 2 góc so le trong do AH // DB )
AB chung
ABHˆ=BADˆ( 2 góc so le trong do AH // DB )
\RightarrowΔABH=ΔBAD( g-c-g )
\Rightarrow AH = BD mà OM=12DB \Rightarrow OM=12AH
\Rightarrow AH = 2 OM ( đpcm )
b) Gọi G' là giao điển của AM và OH, P là trung điểm G'H, Q là trung điểm G'A
Xét Δ AG'H có P là trung điểm G'H, Q là trung điểm G'A \Rightarrow PQ là đường trung bình của \large\Delta AG'H
\RightarrowPQ=12AH và PQ // AH
Do PQ=12AH mà OM=12AH\Rightarrow PQ = OM
Do AH // OM ( cùng ⊥BC ) mà PQ // AH\Rightarrow PQ // OM
Xét ΔPQG′ và ΔOMG′ có
PQG′ˆ=OMG′ˆ( 2 góc so le trong do PQ // OM)
PQ = OM (c/m trên )
QPG′ˆ=MOG′ˆ ( 2 góc so le trong do PQ //OM )
\Rightarrow ΔPQG′=ΔOMG′( g-c-g )
\Rightarrow G'Q = G'M và G'P = G'O
Ta có G'Q = G'M mà G′Q=12G′A( Q là trung điểm G'A ) \Rightarrow G′M=12G′Amà G'M + G'A = AM
\Rightarrow G′A=23AM mà AM là trung tuyến của ΔABC
\Rightarrow G' là trọng tâm của ΔABC ,mà G là trọng tâm của ΔABC \RightarrowG′≡ G
mà G′∈OH \RightarrowG∈OH \Rightarrow O, H, G thẳng hàng ( đpcm )
CM
7 tháng 4 2019
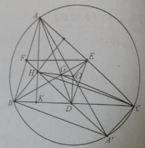
Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F ⇒ biến tam giác ABC thành tam giác DEF.
Đáp án B
TG
17 tháng 10 2021
Trọng tâm : điểm giao nhau của 3 đường trung tuyến trong Tam giác
Trực tâm : giao giữa ba đường cao
Đường trung trực : là đường vuông góc với 1 đoạn thẳng tại trung điểm của đoạn thẳng đó.
chắc giờ trả lời là trễ lắm rồi, 2021 cơ mà. Nhưng lỡ thì kệ đi.
