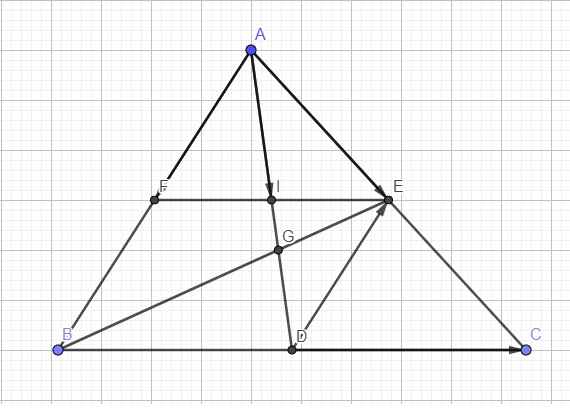
cho tam giác ABC có I là trung điểm của BC và G là trọng tâm . Gọi D và E là hai điểm xác định bởi vecto AD=2 vecto AB và vecto AE = 2/5 vecto AC . Hãy phân tích các vecto DE , DG theo hai vecto AB , AC . Chứng minh ba điểm D,G,E, thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


F là trung điểm AB \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AB}\) ; E là trung điểm AC \(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AC}\)
Ta có EF song song BC (đường trung bình)
Mà D là trung điểm BC \(\Rightarrow\) I là trung điểm EF \(\Rightarrow AI\) là trung tuyến tam giác AEF
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AE}+\dfrac{1}{2}\overrightarrow{AF}\)
Theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{2}{3}\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=\dfrac{2}{3}\overrightarrow{AE}+\dfrac{2}{3}\overrightarrow{AF}\)
DE là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{BA}=-\dfrac{1}{2}\overrightarrow{AB}=-\overrightarrow{AE}\) hay \(\overrightarrow{DE}=-\overrightarrow{AE}+0.\overrightarrow{AF}\)
D là trung điểm BC \(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=-\overrightarrow{AE}+\overrightarrow{AF}\)

a: \(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)

Gọi M là trung điểm EF
\(\overrightarrow{BM}=\dfrac{1}{2}\overrightarrow{BE}+\dfrac{1}{2}\overrightarrow{BF}=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CF}\right)\)
\(=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}-\dfrac{1}{4}\overrightarrow{AB}=-\dfrac{7}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BM}=-\dfrac{7}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{DG}=\overrightarrow{DA}+\overrightarrow{AG}=-\overrightarrow{AD}+\overrightarrow{AG}=-\dfrac{1}{6}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AD}\)

a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\dfrac{-1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
b) CG.CAN??

Ta có \(\overrightarrow{IB}=\overrightarrow{BA}\Rightarrow\hept{\begin{cases}I\in AB\\\overrightarrow{AI}=2\overrightarrow{AB}\end{cases}}\). Tương tự \(\hept{\begin{cases}J\in\left[AC\right]\\\overrightarrow{AJ}=\frac{AJ}{AC}\overrightarrow{AC}=\frac{2}{5}\overrightarrow{AC}\end{cases}}\)
Do đó \(\overrightarrow{IJ}=\overrightarrow{AJ}-\overrightarrow{AI}=\frac{2}{5}\overrightarrow{AC}-2\overrightarrow{AB}\)(đpcm).
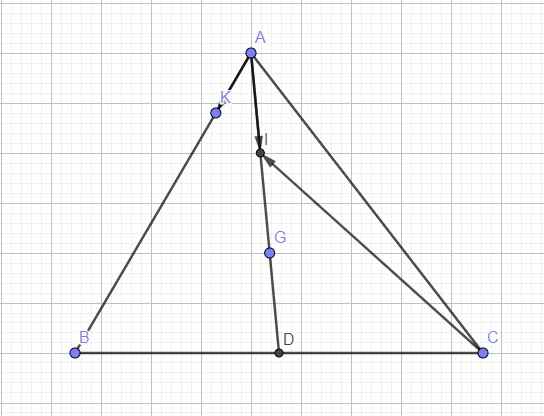
giải giúp t câu này nha : tính vecto IG theo vecto AB và vecto AC (các b vẽ hình ra hộ t nhé)

Do G là trọng tâm tam giác
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}=-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
Do I là trung điểm AG
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)=-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AB}=\dfrac{1}{5}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
\(\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{CA}-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}=\dfrac{4}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)