Một đống cát có hình là một hình chóp tứ giác đều S.ABCD. Cạnh AB = 6m, cạnh bên SA = 5m. Thể tích của đống cát đó là bao nhiêu mét khối ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án A
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Pytago vào tam giác vuông ABC có:
Áp dụng định lí Pytago vào tam giác vuông SAO có:
S O 2 = S A 2 - A O 2 = 13 2 - 5 2 = 144 nên SO = 12cm
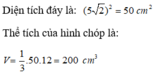


Kiến thức áp dụng
+ Chu vi đường tròn bán kính R là : C = 2πR.
+ Diện tích hình tròn bán kính R là : S = π.R2.

gọi bán kính hình tròn là r.Ta có chu vi hình tròn là \(2r.\pi=12\Rightarrow r=\frac{12}{2\pi}\)
Do đó diện tích hình tròn là \(S=r^2.\pi=\frac{144}{4\pi^2}.\pi=\frac{144}{4\pi}=\frac{144}{4.3,14}\approx11,46m^2\)

Đáp án B
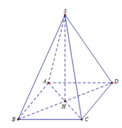
Ta có: 2 B H 2 = a 3 2 ⇒ B H 2 = 3 a 2 2
S H = S B 2 − B H 2 = 2 a 2 − 3 a 2 2 = a 2
Thể tích khối chóp S.ABCD là:
V = 1 3 . S H . S A B C D = 1 3 . a 2 . a 3 2 = a 3 2

Chu vi hình tròn r x 2 x 3,14
Bán kính hình tròn
12 : 3,14 : 2 = 1,9108281 m
Diện tích
1,9108281 x 1,9108281 x 3,14 = 11,464969 m2

Theo giả thiết thì C = 2πR = 12m => R = 12/2Π = 6/Π. Diện tích phần mặt đất mà đống cát chiếm chỗ là: S = Π. R2 = π(6/Π)2 = 36/Π ≈ 11,5 (m2)
Theo giả thiết thì C = 2πR = 12m => R = =
.
Diện tích phần mặt đất mà đống cát chiếm chỗ là:
S = π. R2 = π =
≈ 11,5 (m2)