Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là t/điểm của AD, BC, AC
a)So sánh EK và CD, EF và AB
b)C/m EF\(\le\frac{AB+CD}{2}\)
CÁC BẠN VẼ HÌNH LUN GIÚP MÌNH VỚI NHA!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 9 2021
a) Xét tam giác ADC có:
E là trung điểm AD
K là trung điểm AC
=> EK là đường trung bình
\(\Rightarrow EK=\dfrac{1}{2}CD\)
Xét tam giác ABC có:
F là trung điểm BC(gt)
K là trung điểm AC(gt)
=> KF là đường trung bình
\(\Rightarrow KF=\dfrac{1}{2}AB\)
27 tháng 9 2021
Sửa đề: \(CM:EF\le\dfrac{AB+CD}{2}\)
Ta có: \(EF\le EK+KF=\dfrac{1}{2}AB+\dfrac{1}{2}CD=\dfrac{AB+CD}{2}\)
CM
20 tháng 1 2019
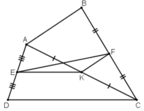
a) + ΔADC có: AE = ED (gt) và AK = KC (gt)
⇒ EK là đường trung bình của ΔADC
⇒ EK = CD/2
+ ΔABC có AK = KC (gt) và BF = FC (gt)
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB/2.
b) Ta có: EF ≤ EK + KF =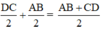 
(Bổ sung: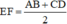 
⇔ EF = EK + KF ⇔ E, F, K thẳng hàng ⇔ AB // CD)
HY
21 tháng 4 2017
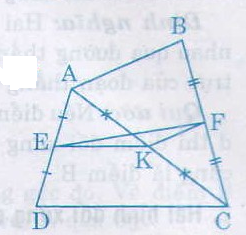
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2 = (AB+CD)/2
Vậy EF ≤ (AB+CD)/2
LH
14 tháng 9 2017
27. Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB.
b) Chứng minh rằng EF \(\le\dfrac{AB+CD}{2}\)
Bài giải:
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK =\(\dfrac{CD}{2}\)
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = \(\dfrac{AB}{2}\)
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = \(\dfrac{CD}{2}\) + \(\dfrac{AB}{2}\) = \(\dfrac{\left(AB+CD\right)}{2}\)
Vậy EF ≤ \(\dfrac{\left(AB+CD\right)}{2}\)
18 tháng 9 2021
a: Xét ΔADC có
E là trung điểm của AD
K là trung điểm của AC
Do đó: EK là đường trung bình của ΔADC
Suy ra: EK//DC và \(EK=\dfrac{DC}{2}\)
Xét ΔABC có
K là trung điểm của AC
F là trung điểm của BC
Do đó: KF là đường trung bình của ΔABC
Suy ra: KF//AB và \(KF=\dfrac{AB}{2}\)
6 tháng 9 2016
bài 1
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2= (AB +CD)/2
Vậy EF ≤ (AB +CD)/2
BN
0
LV
24 tháng 9 2015
EK là đtbinh tam giác => EK=1/2 CD, KF=1/2 AB áp dụng Bđt trong tam giác EKF có EF< EK+KF =>EF< 1/2(AB+CD) . Khi K nằm giữa Evà F thì EF= EK+KF = 1/2(AB+CD) kết hợp cả 2 => đpcm
a) +)EK là đường trung bình nên EK = 1/2 . CD do đó EK < CD
+) EF và AB thì đang suy nghĩ
b) Ta có: \(EK=\frac{1}{2}CD=\frac{CD}{2}\)(t/c đường trung bình)
Tương tự, ta có \(KF=\frac{1}{2}AB\)
Cộng theo vế hai đẳng thức trên ta được:
\(\frac{AB+CD}{2}=EK+KF\ge EF\) ( theo quy tắc 3 điểm)
Đẳng thức xảy ra khi K thuộc EF, khi đó \(\hept{\begin{cases}EK\text{// }CD\\KF\text{//}AB\end{cases}}\) và K thuộc EF nên suy ra \(\hept{\begin{cases}EF\text{//}CD\\EF\text{//}AB\end{cases}}\Leftrightarrow AB\text{//}CD\)
P/s: Chỗ "đẳng thức xảy ra..." mình không chắc.