Cho đường thẳng b song song với đường thẳng c. Đường thẳng d cắt đường thẳng b và c lần lượt tại điểm I và K. Biết rằng ^I4 - ^I1 = 34°.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 6 2016
Kết quả góc = 80 nhé.
Xem thêm tại đây: https://www.facebook.com/groups/giaibaitaponline/permalink/593408784151858/?comment_id=593410360818367¬if_t=group_comment¬if_id=1464852917725746
17 tháng 2 2016
vì ^C1 sole trong với ^B3 (b//c,d cắt b và c) nên ^C1=^B3=90 độ
T
5 tháng 2 2021
bn tự vẽ nha
a. Vì AM vuông góc với CK và AM vuôn góc với BH nên BH// KC
=> KCM = MBH( hai góc so le trong)
Xét tam giác HBM và tam giác KCM có:
HMB = KMC ( hai góc đối đỉnh )
MC = MC ( M là trung điểm của BC)
KCM = MBH (cmt)
Do đó : Tam giác HBM = tam giác KCM ( g-c-g)
=> HM = KM ( hai cạnh tương ứng)
b. Xét Tam giác KBM và tam giác HCM có:
BM = CM ( M là trung điểm của BC)
BMK = CMH ( hai góc đối đỉnh)
MK = MH ( câu a)
Do đó: tam giác KBM = tam giác HCM (c-g-c)
=> BK = HC ( hai cạnh tương ứng )
c. Vì AB // CD nên (GT)
+ ABC = BCD ( hai góc so le trong)
+ DCB = BCA ( hai góc so le trong)
Xét tam giác ABC và tam giác DCB có:
ABC = BCD (cmt)
BC là cạnh chung
DCB = BCA (cmt)
Do đó : Tam giác ABC = tam giác DCB ( g-c-g)
=> CD = BA ( hai cạnh tương ứng )
QD
19 tháng 4 2017
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
19 tháng 4 2017
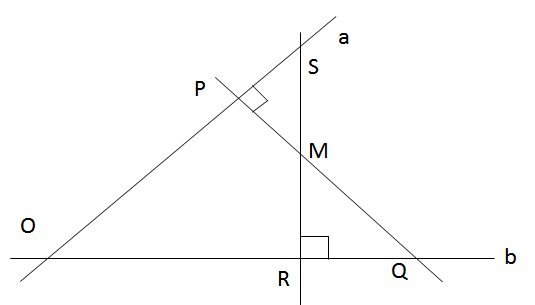
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
