Cho tứ diện ABCD g là điểm trong tam giác BCD k là điểm trong tam giác acd I là điểm thuộc AB cho tìm
(IJK) GIAO (ABD)
(IJK) GIAO (ADC)
(IJK) GIAO (ABC)
(IJK) GIAO (BCD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 1 2019
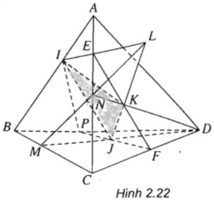
a) Gọi N = DK ∩ AC; M = DJ ∩ BC.
Ta có (DJK) ∩ (ABC) = MN ⇒ MN ⊂ (ABC).
Vì L = (ABC) ∩ JK nên dễ thấy L = JK ∩ MN.
b) Ta có I là một điểm chung của (ABC) và (IJK).
Mặt khác vì L = MN ∩ JK mà MN ⊂ (ABC) và JK ⊂ (IJK) nên L là điểm chung thứ hai của (ABC) và (IJK), suy ra (IJK) ∩ (ABC) = IL.
Gọi E = IL ∩ AC; F = EK ∩ CD. Lí luận tương tự ta có EF = (IJK) ∩ (ACD).
Nối FJ cắt BD tại P; P là một giao điểm (IJK) và (BCD).
Ta có PF = (IJK) ∩ (BCD) Và IP = (ABD) ∩ (IJK)
25 tháng 5 2017
a) Gọi \(N=DK\cap AC;M=DJ\cap BC\).
Ta có \(\left(DJK\right)\cap\left(ABC\right)=MN\Rightarrow MN\subset\left(ABC\right)\)
Vì \(L=\left(ABC\right)\cap JK\) nên dễ thấy \(L=JK\cap MN\)
AH
Akai Haruma
Giáo viên
9 tháng 7 2020
Lởi giải:
a)
Gọi $E$ là giao $AK,CD$. Ta thấy $E\in CD\Rightarrow BE\subset (BCD)$
Gọi $M$ là giao $IK, BE$. Khi đó:
$M\in IK$. $M\in BE\Rightarrow M\in (BCD)$. Do đó $M=IK\cap (BCD)$
b)
Gọi $F$ là giao $DK,AC$, $H$ là giao $DJ, BC$
$\Rightarrow FH\subset (ABC)$. Lấy $G$ là giao điểm $FH, JK$ thì ta thấy:
$G\in FH\Rightarrow G\in (ABC)$
$G\in JK\Rightarrow G\in (IJK)$
$I\in AB\Rightarrow I\in (ABC)$
$I\in (IJK)$
$\Rightarrow GI$ là giao tuyến của $(IJK)$ và $(ABC)$
c)
Giao tuyến của $(IJK)$ và $(ACD)$
Gọi $L$ là giao $IG, AC$.
$L\in IG\Rightarrow L\in (IJK)$
$L\in AC\Rightarrow L\in (ACD)$
Mà $E\in IK\Rightarrow E\in (IJK)$
$E\in CD\Rightarrow E\in (ACD)$
Do đó $EL$ là giao tuyến của $(IJK)$ và $(ACD)$
------------------
Giao tuyến của $(IJK)$ và $(ABD)$
Gọi $P$ là giao điểm $EJ$ và $BD$
$P\in BD\Rightarrow P\in (ABD)$
$P\in EJ\Rightarrow P\in (IJK)$
$I\in (IJK)$ và $I\in (ABD)$
$\Rightarrow PI$ là giao tuyến $(ABD)$ và $(IJK)$
------------------
Giao tuyến $(IJK)$ và $(BCD)$
$E\in IK\Rightarrow E\in (IJK)$
$E\in CD\Rightarrow E\in (BCD)$
$P\in (IJK)$ và $P\in BD\Rightarrow P\in (BCD)$
Do đó $PE$ là giao tuyến $(IJK)$ và $(BCD)$
Bạn tự vẽ hình.
CM
7 tháng 2 2018
Đáp án C
Mặt phẳng (ABD) cắt mặt phẳng (IJK) theo giao tuyến song song với AB do IJ//AB
CM
11 tháng 7 2019
Đáp án C
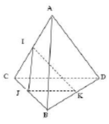
Mặt phẳng (ABD) cắt mặt phẳng (IJK) theo giao tuyến song song với AB do IJ//AB
