Cho 6điểm A,B,C,D,E,F .CMR
A, vector AD + vector BE + vectơ CF = vector AE+ Vectơ BF+ Vectơ CD = vector AF + VECTO BD + vectơ CE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NV
Ngân Vũ Thị
5 tháng 8 2019
https://i.imgur.com/6Olhnm4.jpg
Đúng(0)
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 9 2020
Chưa đủ dữ kiện đề bài để chứng minh đẳng thức. Bạn xem lại đề.
AH
Akai Haruma
Giáo viên
22 tháng 10 2020
Lời giải:
a)
$2\overrightarrow{AD}=\overrightarrow{AD}+\overrightarrow{AD}$
$=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{CD}$
$=\overrightarrow{AB}+\overrightarrow{AC}+(\overrightarrow{BD}+\overrightarrow{CD})$
$=\overrightarrow{AB}+\overrightarrow{AC}$
$\Rightarrow \overrightarrow{AD}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$
Tương tự:
$\overrightarrow{BE}=\frac{\overrightarrow{BC}+\overrightarrow{BA}}{2}$
$\overrightarrow{CF}=\frac{\overrightarrow{CA}+\overrightarrow{CB}}{2}$
Cộng lại:
$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\frac{\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{CB}}{2}=\frac{\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}}{2}=\overrightarrow{0$}$
Ta có đpcm.
b)
$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MD}+\overrightarrow{DA}+\overrightarrow{ME}+\overrightarrow{EB}+\overrightarrow{MF}+\overrightarrow{FC}$
$=(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF})+(\overrightarrow{DA}+\overrightarrow{EB}+\overrightarrow{FC})$
$=(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF})-(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF})$
$=\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}-\overrightarrow{0}$ (theo phần a)
$=\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}$
Ta có đpcm.
CM
23 tháng 8 2017
+ Trong không gian, hai đường thẳng chéo nhau vẫn có thể vuông góc với nhau.
Đường thẳng a có vectơ chỉ phương u →
Đường thẳng b có vectơ chỉ phương v →
3 tháng 9 2022
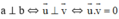
Câu 1:
Gọi M là trung điểm của AC
AM=AC/2=2
\(BM=\sqrt{3^2+2^2}=\sqrt{13}\)
\(\left|\overrightarrow{AB}+\overrightarrow{CB}\right|=\left|\overrightarrow{BA}+\overrightarrow{BC}\right|=2\cdot BM=2\sqrt{13}\)
Câu 6:
\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EF}+\overrightarrow{FA}\)
\(=\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{EA}=\overrightarrow{AE}+\overrightarrow{EA}=\overrightarrow{0}\)
