Hỗn hợp X chứa Fe và Cu có tỉ lệ mol tương ứng là 1:2 . Số mol của Fe và Cu có trong 27,6 g hỗn hợp X lần lượt là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình ghi đáp án thôi nhé
1 .
nFe = 0.15 mol
nCu = 0.3 mol
2.
nFeO = 0.04 mol
nFe2O3 = 0.08 mol
3.
nCuO = 0.06 mol
nFe2O3 = 0.12 mol
4.
nMgCO3 = nCaCO3 = 0.1 mol
5.
nNaOH = 0.4 mol
nKOH = 0.2 mol
%NaOH = 66.67%
%KOH = 33.33%
6.
nO2 = 0.3 mol
nCl2 = 0.15 mol
7.
nO2 = 0.4 mol
nCl2 = 0.2 mol

F22: Tính số mol mỗi kim loại ? Biết :
a. 9,96 gam hỗn hợp X ( Fe , Al có tỷ lệ mol 1 : 1) .
Gọi x, y lần lượt là số mol Fe, Al
\(\left\{{}\begin{matrix}56x+27y=9,96\\x=y\end{matrix}\right.\)
=> x=y= 0,12(mol)
b. 27,6 gam hỗn hợp Y ( Fe , Cu có tỷ lệ mol 1 : 2) .
Gọi x, y lần lượt là số mol Fe, Cu
\(\left\{{}\begin{matrix}56x+64y=27,6\\\dfrac{x}{y}=\dfrac{1}{2}\end{matrix}\right.\)
=> x= 0,15; y=0,3
c. 29,52 gam hỗn hợp Z ( Cu, Al có tỷ lệ mol 3 : 2 ) .
Gọi x, y lần lượt là số mol Cu, Al
\(\left\{{}\begin{matrix}64x+27y=29,52\\\dfrac{x}{y}=\dfrac{3}{2}\end{matrix}\right.\)
=> x= 0,36 ; y=0,24
F23: 11 gam hỗn hợp X (Al, Fe) có tổng số mol là 0,3. Tính khối lượng mỗi kim loại ?
Gọi x, y lần lượt là số mol Al, Fe
\(\left\{{}\begin{matrix}27x+56y=11\\x+y=0,3\end{matrix}\right.\)
=> x=0,2 , y =0,1
=> \(\left\{{}\begin{matrix}m_{Al}=0,2.27=5,4\left(g\right)\\m_{Fe}=0,1.56=5,6\left(g\right)\end{matrix}\right.\)

$n_{Mg}+n_{Fe}=n_X=0,3$
Mà $n_{Mg}:n_{Fe}=2:1$
$\to n_{Mg}=2n_{Fe}$
$\to 2n_{Fe}+n_{Fe}=0,3$
$\to n_{Fe}=0,1(mol)$
$\to n_{Mg}=0,2(mol)$
$\to m_{hỗn\,hợp}=0,2.24+0,1.56=10,4(g)$

Đáp án C
Ta có nN2O = 0,1 mol; nNO = 0,2 mol và nNO2 = 0,3 mol
Có mmuối = mkl + mNO3- = 100 + 62. ( 0,1. 8 + 0,2. 3+ 0,3) = 205,4 gam
Có nHNO3 pư = 0,1.10 + 0,2. 4 + 0.3.2 = 2,4 mol





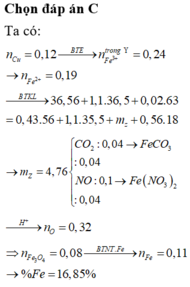
gọi a, b lần lượt là số mol của Fe và Cu có trong hỗn hợp X
ta có: 56a+ 64b= 27,6 (1)
theo giả thiết: nFe: nCu= 1: 2
\(\Rightarrow\) a: b= 1: 2 \(\Rightarrow\) 2a= b
thay 2a= b và (1) có: 56a+ 64.2b= 27,6
\(\Rightarrow\) a= 0,15( mol)
\(\Rightarrow\) b=0,3( mol)
gọi nFe=a nCu=b
\(\left\{{}\begin{matrix}\frac{a}{b}=\frac{1}{2}\\56a+64b=27,6\end{matrix}\right.\)=> a=0,15 b=0,3