x(4x2-1)=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
10 tháng 7 2021
Lời giải:
$4x^2-2x-1=0$
$\Leftrightarrow [(2x)^2-2.2x.\frac{1}{2}+(\frac{1}{2})^2]-\frac{5}{4}=0$
$\Leftrightarrow (2x-\frac{1}{2})^2=\frac{5}{4}$
$\Rightarrow 2x-\frac{1}{2}=\pm \frac{\sqrt{5}}{2}$
$\Leftrightarrow 2x=\frac{1\pm \sqrt{5}}{2}$
$\Rightarrow x=\frac{1\pm \sqrt{5}}{4}$
$x^4-4x^2-32=0$
$\Leftrightarrow (x^2-2)^2-36=0$
$\Leftrightarrow (x^2-2-6)(x^2-2+6)=0$
$\Leftrightarrow (x^2-8)(x^2+4)=0$
Vì $x^2+4>0$ với mọi $x$ nên $x^2-8=0$
$\Leftrightarrow x=\pm 2\sqrt{2}$
10 tháng 7 2021
a) Ta có: \(4x^2-2x-1=0\)
\(\Delta=\left(-2\right)^2-4\cdot4\cdot\left(-1\right)=4+16=20\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{2-2\sqrt{5}}{8}=\dfrac{1-\sqrt{5}}{4}\\x_2=\dfrac{2+2\sqrt{5}}{8}=\dfrac{1+\sqrt{5}}{4}\end{matrix}\right.\)
b) Ta có: \(x^4-4x^2-32=0\)
\(\Leftrightarrow x^4-8x^2+4x^2-32=0\)
\(\Leftrightarrow x^2=8\)
hay \(x\in\left\{2\sqrt{2};-2\sqrt{2}\right\}\)
em c.ơn trước
CM
10 tháng 2 2018
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
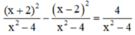
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
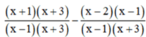
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
PN
15 tháng 5 2021
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
13 tháng 11 2021
\(a,\Leftrightarrow x\left(2x-7\right)+2\left(2x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(2x-7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{7}{2}\end{matrix}\right.\\ b,\Leftrightarrow x\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ c,\Leftrightarrow\left(2x-1\right)\left(2x+1\right)-2\left(2x-1\right)^2=0\\ \Leftrightarrow\left(2x-1\right)\left(2x+1-4x+2\right)=0\\ \Leftrightarrow\left(2x-1\right)\left(-2x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\\ d,\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
16 tháng 2 2022
\(\Leftrightarrow4x^2\left(x-1\right)-\left(x-1\right)=0\Leftrightarrow\left(2x-1\right)\left(2x+1\right)\left(x-1\right)=0\Leftrightarrow x=\dfrac{1}{2};x=-\dfrac{1}{2};x=1\)
TD
16 tháng 2 2022
\(4x^3-4x^2-x+1=0\)
<=>\(\left(2x+1\right)\left(x-1\right)\left(2x-1\right)=0\)
<=>\(\left[{}\begin{matrix}x=\dfrac{-1}{2}\\x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)
13 tháng 2 2022
\(a,\left(x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\\ b,4x^2-1=0\\ \Leftrightarrow\left(2x-1\right)\left(2x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-1=0\\2x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
\(c,x^2-4x+3=0\\ \Leftrightarrow x^2-3x-x+3=0\\ \Leftrightarrow x\left(x-3\right)-\left(x-3\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
\(d,9x^2-6x+1=0\\ \Leftrightarrow\left(3x-1\right)^2=0\\ \Leftrightarrow3x-1=0\\ \Leftrightarrow x=\dfrac{1}{3}\)
\(x\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\4x^2-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\frac{1}{2}\\x=\frac{1}{2}\end{matrix}\right.\)
cho mk hỏi là 4 nhân 2 hay 4x nhân 2