Cho 2 đường tròn ( O ) và ( O' ) tiếp xúc ngoài tại S . Kẻ các tiếp tuyến ngoài AB và CD với A , B thuộc ( O ) và B , D thuộc ( O' ) .
Chứng minh : AB + CD = AC + BD .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

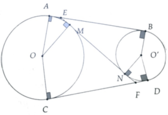
a, Ta có AB = AE + BE = EM + EN
Và CD = FD + FC = NF + NE
=> AB + CD = 2EF => AB = EF
b, Ta có EM = AB – EB = EF – EN = NF
Gọi tiếp tuyến chung tại S của (O) và (O') cắt AB tại T. OO' cắt AC,BD lần lượt tại E,F.
Vì AB,CD là tiếp tuyến chung ngoài của (O) và (O') nên ABDC là hình thang cân có trục đối xứng OO'
Từ đó AB = CD và E,F lần lượt là trung điểm của AC,BD
Dễ thấy AT = BT = ST => T là trung điểm AB. Suy ra ST là đường trung bình của hình thang AEFB
=> AB = 2ST = AE + BF = (AC + BD)/2. Mà CD = AB (cmt) nên AB + CD = AC + BD (đpcm).