Một ôtô dự định đi từ A đến B với vận tốc 40km/h. Lúc đầu ôtô đi với vận tốc đó .Khi còn 60 km nữa thì được nửa quãng đường ôtô tăng vận tốc lên là 50km/h nên đến sớm hơn dự định 1 giờ. Tính quãng đường AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vận tốc của otoo trong nữa quãng đường còn lại
40km/h + 10km/h = 50km/h
Nửa quãng đường đầu ô tô đi mất :
60 : 40 = 1,5 giờ = 1 giờ 30 phút
Nửa quãng đường sau ô tô đi mất :
60 : 50 = 1,2 giờ = 1 giờ 12 phút
Tổng thời gian cả 2 lần đi :
1 giờ 30 phút + 1 giờ 12 phút = 2 giờ 42 phút = 2,7 giờ
Thời gian ô tô dự định đi :
2,7 + 1 = 3,7 (giờ)
Từ đó ta có thể suy ra được quãng đường AB :
40 x 3,7 =148 (km)
Đáp số : 148 km

Gọi quãng đường AB là x (km) (x>0)
thì số thời gian dự định của ô tô là x/40 (km)

theo cậu là :
280 km
à cậu tự trả lời chứng tỏ là biết rồi thì hỏi làm
chi

Bài 24:
Gọi x(km/h) và y(h) lần lượt là vận tốc và thời gian ô tô ban đầu dự định đi từ A đến B(Điều kiện: x>0; y>0)
Độ dài quãng đường AB là: xy(km)
Vì khi vận tốc ô tô tăng thêm 10km/h thì đến B sớm hơn 30 phút so với dự định nên ta có phương trình:
\(\left(x+10\right)\left(y-\dfrac{1}{2}\right)=xy\)
\(\Leftrightarrow xy-\dfrac{1}{2}x+10y-5=xy\)
\(\Leftrightarrow xy-\dfrac{1}{2}x+10y-5-xy=0\)
\(\Leftrightarrow\dfrac{-1}{2}x+10y=5\)(1)
Vì khi vận tốc ô tô giảm đi 5km/h thì đến B muộn 20 phút so với dự định nên ta có phương trình:
\(\left(x-5\right)\left(y+\dfrac{1}{3}\right)=xy\)
\(\Leftrightarrow xy+\dfrac{1}{3}x-5y-\dfrac{5}{3}=xy\)
\(\Leftrightarrow xy+\dfrac{1}{3}x-5y-\dfrac{5}{3}-xy=0\)
\(\Leftrightarrow\dfrac{1}{3}x-5y=\dfrac{5}{3}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{-1}{2}x+10y=5\\\dfrac{1}{3}x-5y=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-1}{6}x+\dfrac{10}{3}y=\dfrac{5}{3}\\\dfrac{1}{6}x-\dfrac{5}{2}y=\dfrac{5}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{6}y=\dfrac{5}{6}\\\dfrac{1}{3}x-5y=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\\dfrac{1}{3}x=\dfrac{5}{3}+5y=\dfrac{5}{3}+5=\dfrac{20}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=20\\y=1\end{matrix}\right.\)(thỏa ĐK)
Độ dài quãng đường AB là:
\(xy=20\cdot1=20\left(km\right)\)
Vậy: Quãng đường AB dài 20km
Bài 25:
Gọi vận tốc xe đi từ A và xe đi từ B lần lượt là a, b(km/h; a>10; b>0; a>b)
Mỗi giờ xe đi từ A đi nhanh hơn xe kia 10km => a - b = 10 (1)
Sau 5 giờ xe đi từ A đi được: 5a (km)
Sau 5 giờ xe đi từ B đi được: 5b (km)
Nếu đi ngược chiều, 2 xe gặp nhau sau 5 giờ nên ta có: 5a+5b=350 (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{{}\begin{matrix}a-b=10\\5a+5b=350\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}5a-5b=50\\5a+5b=350\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}10a=400\\a-b=10\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}a=40\\b=30\end{matrix}\right.\) (tm)
Vậy vận tốc của xe đi từ A và xe đi từ B lần lượt là 40km/h và 30km/h
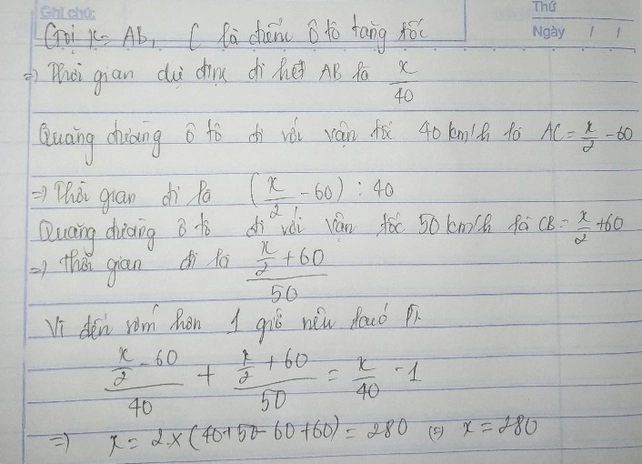
Gọi quãng đường AB là x(km, x>0)
thời gian dự định của ô tô là x/40 (h)
thời gian thực tế là (x/2-60)/40 + (x/2+60)/50+40
Theo bài ra ta có pt
x/40-[(x/2-60)/40+(x/2+60)/90)=1
r tự giải pt r kết luận đi nka ^^