Cho hình vuông ABCD, một góc xAy = 45 độ có Ax cắt BC tại E, Ay cắt CD tại F. Trên tia đối của tia DC lấy điểm G sao cho GD = BI
a, Tính góc FAG
b, CMR : BE + DF = FE
Giải dc nhanh tr 1h sẽ dc 10SP 1 GP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
9 tháng 2 2018
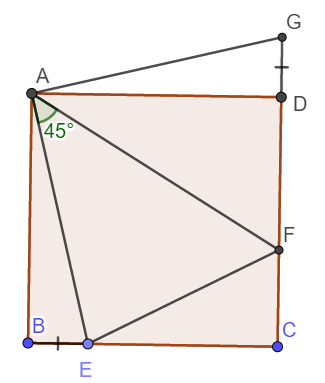
a) Xét tam giác vuông ABE và ADG có:
BE = DG (gt)
AB = AD
\(\Rightarrow\Delta ABE=\Delta ADG\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{BAE}=\widehat{DAG}\) (Hai góc tương ứng)
\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{DAG}+\widehat{FAD}\)
\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{FAG}\)
Mà \(\widehat{BAE}+\widehat{FAD}=90^o-\widehat{EAF}=45^o\) nên \(\widehat{FAG}=45^o\)
b) Do \(\Delta ABE=\Delta ADG\Rightarrow AE=AG\)
Xét tam giác AEF và AGF có:
AE = AG (cmt)
Cạnh AF chung
\(\widehat{EAF}=\widehat{GAF}\left(=45^o\right)\)
\(\Rightarrow\Delta AEF=\Delta AGF\left(c-g-c\right)\)
\(\Rightarrow EF=GF=FD+DG=FD+BE\)
3 tháng 3 2022
Xét ΔABC và ΔADE có
AB=AD
\(\widehat{BAC}\) chung
AC=AE
Do đó: ΔABC=ΔADE
Suy ra: \(\widehat{MCD}=\widehat{MEB}\)
Xét ΔCBE và ΔEDC có
CB=ED
CE chung
BE=DC
Do đó: ΔCBE=ΔEDC
Suy ra: \(\widehat{MBE}=\widehat{MDC}\)
Xét ΔMBE và ΔMDC có
\(\widehat{MBE}=\widehat{MDC}\)
BE=DC
\(\widehat{MEB}=\widehat{MCD}\)
Do đó: ΔMBE=ΔMDC
Suy ra: ME=MC
Xét ΔAME và ΔAMC có
AM chung
ME=MC
AE=AC
Do đó: ΔAME=ΔAMC
Suy ra: \(\widehat{EAM}=\widehat{CAM}\)
hay AM là tia phân giác của góc xAy
14 tháng 12 2021
Gọi giao điểm của IK và FE là O
ΔIOE và ΔFOK cùng vuông tại O có:
DE chung
IEOˆ=OFKˆ (vì IE // CD)
ΔIOE = ΔFOK (cgv - gnk)
=> IE = KF (tương ứng)
Có: F,KϵCDF,KϵCD mà IE // CD => KF // IE
Xét tứ giác FIEK có:
IE // KF (cmt)
IE = KF (cmt)
FIEK là hình bình hành (dhnb) có 2 đường chéo IK ⊥⊥ FE (gt) \Rightarrow FIEK là hình thoi
NN
25 tháng 11 2018
Bài 1:
Do E là hình chiếu của D trên AB:
=) DE\(\perp\)AB tại E
=) \(\widehat{DE\text{A}}\)=900
Do F là hình chiếu của D trên AC:
=) DF\(\perp\)AC
=) \(\widehat{DFA}\)=900
Xét tứ giác AEDF có :
\(\widehat{D\text{E}F}\)=\(\widehat{E\text{A}F}\)=\(\widehat{DFA}\) (cùng bằng 900)
=) Tứ giác AEDF là hình chữ nhật
Xét hình chữ nhật AEDF có :
AD là tia phân giác của \(\widehat{E\text{A}F}\)
=) AEDF là hình vuông
DV
8 tháng 12 2016
HÌNH BẠN TỰ VẼ NHÉ
Tam giác BAD có góc BAD bằng 90 độ => góc ABD + góc ADB =90 độ
lại có: Góc FAD là góc ngoài của tam giác BAD tại đỉnh A
\(\Rightarrow\)góc FAD = góc ABD + góc ADB
= 90 độ
Mật khác: góc BAF = góc BAD + góc DAF
= 90 độ + 90 độ
= 180 độ
=> B,A,F thẳng hàng
31 tháng 7 2015
a) Xét tam giác ABD và EBD có:
- AB=BE (gt)
- góc ABD = góc EBD ( BD là phân giác góc B)
- Chung cạnh BD
=> Tam giác ABD = tam giác EBD (c.g.c)
=> DA = DE ( 2 cạnh tương ứng)
