hàm số y=5+4sin2xcos2x có tất cả bao nhiêu giá trị nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Nhắc lại quy tắc vẽ đồ thị hàm số y = f x từ đồ thị hàm số y = f x
- Phần 1: Giữ nguyên phần đồ thị hàm số y = f x bên phải trục Oy (bỏ phần bên trái)
- Phần 2: Lấy đối xứng phần đồ thị hàm số y = f x bên phải trục O qua trục O
- Hợp của 2 phần, ta được đồ thị hàm số y = f x
Xét y = f x = 1 3 x 3 − 2 x 2 + m − 1 x + 3 với f x = 1 3 x 3 − 2 x 2 + m − 1 x + 3
Để hàm số y = f x có 5 điểm cực trị ⇔ y = f x có 2 điểm cực trị nằm phía bên phải trục Oy ⇔ f ' x = 0 có 2 nghiệm dương phân biệt ⇔ x 2 − 4 x + m − 1 = 0 có 2 nghiệm dương phân biệt x 1 , x 2
⇔ Δ > 0 x 1 + x 2 > 0 x 1 x 2 > 0 ⇔ 5 − m > 0 m − 1 > 0 ⇔ 1 < m < 5 . Kết hợp m ∈ ℤ → m = 2 ; 3 ; 4

Để hàm số ![]() có đúng 3 cực trị thì hàm số
có đúng 3 cực trị thì hàm số ![]() có 2 cực trị trái dấu.
có 2 cực trị trái dấu.
Trước hết cần điều kiện m-1≠0
⇔m≠1
Ta có ![]()
Để hàm số
![]() có 2 cực trị trái dấu thì phương trình y'=0 có 2 nghiệm trái dấu
có 2 cực trị trái dấu thì phương trình y'=0 có 2 nghiệm trái dấu ![]()
Kết hợp điều kiện ![]()
Khi m=1 thì hàm số trở thành ![]() có 1 cực trị Khi đó hàm số
có 1 cực trị Khi đó hàm số ![]() có đúng 3 điểm cực trị.
có đúng 3 điểm cực trị.
Vậy m∈-2;-1;0;1
Chọn C

TXĐ: D = R .
TH1: m = 1 . Khi đó hàm số trở thành:
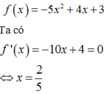
BBT:
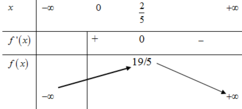
Từ đó ta suy ra BBT của hàm số y = f x như sau:
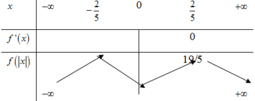
Hàm số có 3 điểm cực trị, do đó m = 1 thỏa mãn.
TH2: m ≠ 1 Để hàm số y = f x có 3 điểm cực trị thì hàm số y = f x có 2 điểm cực trị trái dấu.
Ta có:
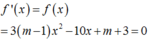
Để hàm số có 2 cực trị trái dấu ⇔ f x = 0 có 2 nghiệm trái dấu

Chọn B.




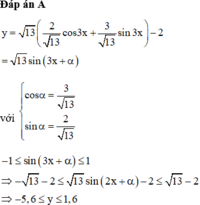


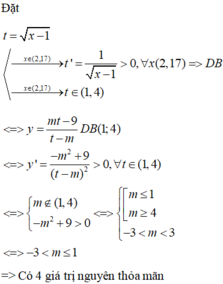



Lời giải:
\(y=5+4\sin 2x\cos 2x=5+2\sin 4x\)
Ta thấy \(\sin 4x\in [-1;1], \forall x\in\mathbb{R}\Rightarrow 2\sin 4x\in [-2;2]\)
Để $y$ nhận giá trị nguyên thì $2\sin 4x$ phải nhận giá trị nguyên. Mà trong đoạn $[-2;2]$ có $5$ giá trị nguyên nên $y$ cũng có tất cả $5$ giá trị nguyên.
cho hỏi là trên 5+2sin4x nhưng sao chỉ tìm giá trị của 2sin4x vậy ạ ?