Cho tam giác nhọn ABC có AD và BE là hai đường cao cắt nhau tại H.
a) Cho biết góc ABC > góc ACB. Chứng minh rằng HC > HB
b) Vẽ HF vuông góc AB tại F. Chứng minh rằng ba điểm C, H, F thẳng hàng
c) Chứng minh rằng AB + AC > 2AD
d) Chứng minh rằng HA + HB + HC < 2/3 ( AB + AC + BC )
AI GIẢI NHANH VÀ ĐÚNG MIK SẼ TICK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 5 2021
a) Xét ΔAEH vuông tại E và ΔBDH vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)(hai góc đối đỉnh)
Do đó: ΔAEH\(\sim\)ΔBDH(g-g)
5 tháng 7 2021
Sửa đề: ΔABC vuông tại A
a) Xét ΔDAB vuông tại D và ΔACB vuông tại A có
\(\widehat{ABC}\) chung
Do đó: ΔDAB\(\sim\)ΔACB(g-g)
b) Xét ΔABC có
BE là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AE}{EC}=\dfrac{AB}{BC}\)(Định lí đường phân giác của tam giác)(1)
Ta có: ΔDAB\(\sim\)ΔACB(cmt)
nên \(\dfrac{AB}{BC}=\dfrac{BD}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)(2)
Từ (1) và (2) suy ra \(\dfrac{AE}{EC}=\dfrac{BD}{AB}\)
hay \(AE\cdot AB=BD\cdot EC\)(đpcm)
10 tháng 3 2023
a: Xét ΔAFH vuông tại F và ΔADB vuông tại D có
góc FAH chung
=>ΔAFH đồng dạng ΔADB
b: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AFE=góc ACB
mà góc FAE chung
nên ΔAFE đồng dạng với ΔACB
góc FEH=góc BAD
góc DEH=góc FCB
mà góc BAD=góc FCB
nên góc FEH=góc DEH
=>EH là phân giác của góc FED
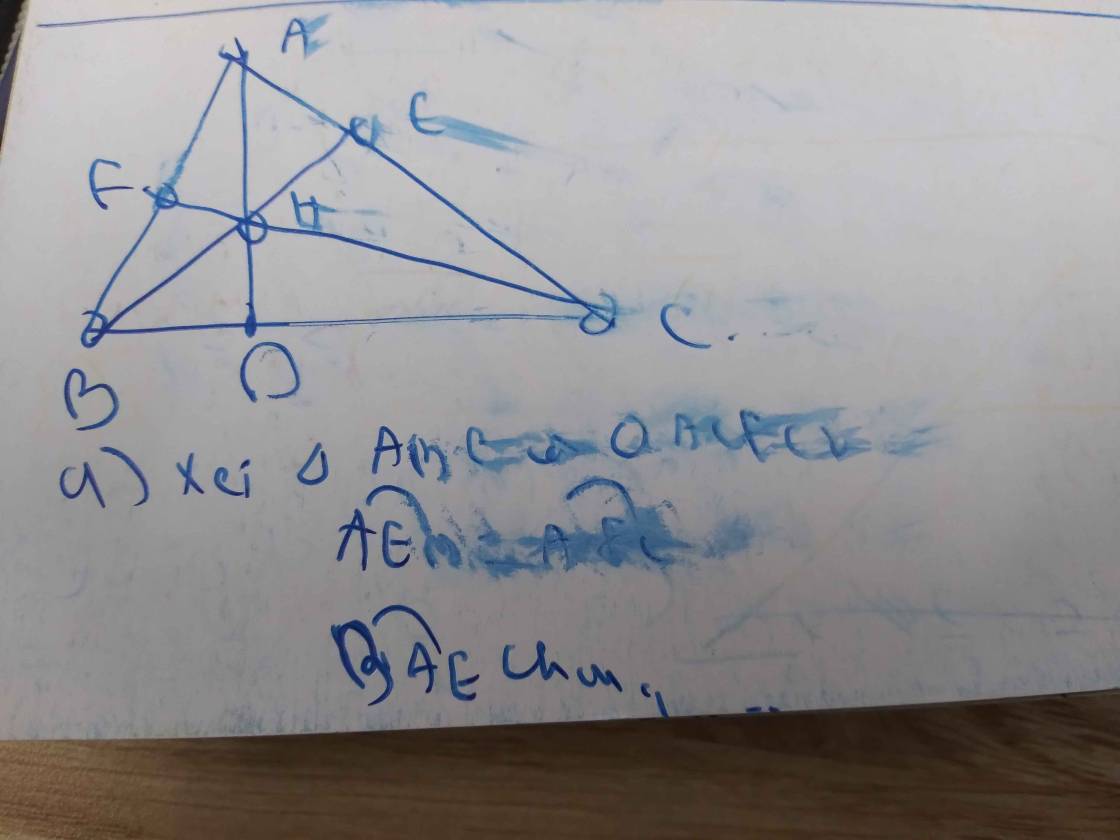
Tam giác ABC có : góc ABC > góc ACB (gt)
=> AC > AB (đl)
AD _|_ BC (gt)
D thuộc BC
=> BD < DC
H thuộc AD
=> HB < HC
b, AD; BE là đường cao
ADcắt BE tại H
=> CH là đường cao (đl)
=> CH _|_ AB (đn)
HF _|_ AB (gt)
=> C; H; F thẳng hàng
c.
\(AB>AD;AC>AD\left(ch>cgv\right)\)
\(\Rightarrow AB+AC>2AD\left(đpcm\right)\)
d
Kẻ \(HN//AC;HM//AB\)
Theo tính chất cặp đoạn chắn,ta có:\(HM=AN\)
Áp dụng bất đẳng thức tam giác ta có:
\(HA< AM+HM=AM+AN\left(1\right)\)
Do \(BH\perp AC;HN//AC\Rightarrow NH\perp HN\)
Xét \(\Delta BHN\) ta có:\(BH< BN\left(2\right)\)
Tương tự trong tam giác CHM có \(CH< CM\left(3\right)\)
Tiừ \(\left(1\right);\left(2\right);\left(3\right)\Rightarrow HA+HB+HC< AM+AN+BN+CM=AB+AC\)
Tương tự,ta có:
\(HA+HB+HC< AB+BC\)
\(HA+HB+HC< BC+AC\)
\(\Rightarrow3\left(HA+HB+HC\right)< 2\left(AB+BC+CA\right)\)
\(\Rightarrow HA+HB+HC< \frac{2}{3}\left(AB+BC+CA\right)\)