giải phương trình sau:\(\left(1+\sqrt{x^2+2020x}+2019\right)\left(\sqrt{x+2019}-\sqrt{x+1}\right)=2018\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
giải phương trình:\(\left(1+\sqrt{x^2+2020x}+2019\right)\left(\sqrt{x+2019}-\sqrt{x+1}\right)=2018\)
0
LG
28 tháng 11 2019
Từ hệ phương trình \(\Rightarrow\left(\sqrt{x-2018}-\sqrt{x-2019}\right)+\left(\sqrt{y-2018}-\sqrt{y-2019}\right)=2\)
Ta có: \(\sqrt{x-2018}-\sqrt{x-2019}\le\sqrt{\left(x-2018\right)-\left(x-2019\right)}=1\) Dấu = xảy ra khi và chỉ khi x = 2019
Tương tự: \(\sqrt{y-2018}-\sqrt{y-2019}\le1\)
Dấu = xảy ra khi và chỉ khi y = 2019
Nên: \(\left(\sqrt{x-2018}-\sqrt{x-2019}\right)+\left(\sqrt{y-2018}-\sqrt{y-2019}\right)\le2\)
Dấu = xảy ra khi và chỉ khi \(\left\{{}\begin{matrix}x=2019\\y=2019\end{matrix}\right.\)
Kết luận nghiệm pt: \(\left\{{}\begin{matrix}x=2019\\y=2019\end{matrix}\right.\)
9 tháng 2 2021
ĐKXĐ : \(\left\{{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)
- Từ PT ( I ) ta có : \(x-1+2\sqrt{xy}-2\sqrt{y}=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)+2\sqrt{y}\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x}+1+2\sqrt{y}\right)=0\)
Thấy : \(\sqrt{x}+2\sqrt{y}+1\ge1>0\)
\(\Rightarrow\sqrt{x}-1=0\)
\(\Leftrightarrow x=1\)
- Thay x = 1 vào PT ( II ) ta được :
\(y=2019-x=2019-1=2018\)
Vậy ...
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2018
\(x\left(\sqrt{2019}+\sqrt{2018}\right)+y\left(\sqrt{2019}-\sqrt{2018}\right)=2019\sqrt{2019}+2018\sqrt{2018}\)
\(\Leftrightarrow x\left(\sqrt{2019}+\sqrt{2018}\right)+y\left(\sqrt{2019}-\sqrt{2018}\right)=2018\left(\sqrt{2019}+\sqrt{2018}\right)+\sqrt{2019}\)
\(\Leftrightarrow x+y.\left(\sqrt{2019}-\sqrt{2018}\right)^2=2018+\sqrt{2019}\left(\sqrt{2019}-\sqrt{2018}\right)\)
\(\Leftrightarrow x+y\left(4037-2\sqrt{2019.2018}\right)=4037-\sqrt{2019.2018}\)
\(\Leftrightarrow x+4037.y-4037=2y\sqrt{2019.2018}-\sqrt{2019.2018}\)
\(\Leftrightarrow x+4037y-4037=\left(2y-1\right).\sqrt{2019.2018}\)(1)
Do \(x;y\) hữu tỉ \(\Rightarrow x+4037y-4037\) và \(2y-1\) đều là số hữu tỉ
Mà \(\sqrt{2019.2018}\) là số vô tỉ
\(\Rightarrow\)đẳng thức (1) xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}2y-1=0\\x+4037y-4037=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y=\dfrac{1}{2}\\x=\dfrac{4037}{2}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 9 2019
ĐKXĐ: \(x\ge-4\)
\(\Leftrightarrow\sqrt{x+5}-\sqrt{\left(x+5\right)\left(x+4\right)}+2019\sqrt{x+4}-2019=0\)
\(\Leftrightarrow\sqrt{x+5}\left(1-\sqrt{x+4}\right)-2019\left(1-\sqrt{x+4}\right)=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-2019\right)\left(1-\sqrt{x+4}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x+4}=1\\\sqrt{x+5}=2019\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-3\\x=2019^2-5\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 11 2021
Chú ý:
\(\left(x^2+2x\right)^2+4\left(x+1\right)^2=\left(x^2+2x\right)^2+4\left(x^2+2x+1\right)=\left(x^2+2x\right)^2+4\left(x^2+2x\right)+4\)
\(=\left(x^2+2x+2\right)^2\)
\(x^2+\left(x+1\right)^2+\left(x^2+x\right)^2\)
\(=\left(x^2+x\right)+x^2+x^2+2x+1\)
\(=\left(x^2+x\right)^2+2x^2+2x+1\)
\(=\left(x^2+x\right)^2+2\left(x^2+x\right)+1\)
\(=\left(x^2+x+1\right)^2\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 9 2019
ĐKXĐ: ...
Đặt \(\left(\sqrt{x-2018};\sqrt{y-2019};\sqrt{z-2020}\right)=\left(a;b;c\right)\) \(\Rightarrow a;b;c>0\)
\(\frac{a-1}{a^2}+\frac{b-1}{b^2}+\frac{c-1}{c^2}=\frac{3}{4}\)
\(\Leftrightarrow\frac{4a-4}{a^2}+\frac{4b-4}{b^2}+\frac{4c-4}{c^2}=3\)
\(\Leftrightarrow1-\frac{4a-a}{a^2}+1-\frac{4b-4}{b^2}+1-\frac{4c-4}{c^2}=0\)
\(\Leftrightarrow\frac{a^2-4a+4}{a^2}+\frac{b^2-4b+4}{b^2}+\frac{c^2-4c+4}{c^2}=0\)
\(\Leftrightarrow\left(\frac{a-2}{a}\right)^2+\left(\frac{b-2}{b}\right)^2+\left(\frac{c-2}{c}\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-2=0\\b-2=0\\c-2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=2\\c=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{x-2018}=2\\\sqrt{y-2019}=2\\\sqrt{z-2020}=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2022\\y=2023\\z=2024\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 9 2019
\(2x^2+4x+2=21-3y^2\)
\(\Leftrightarrow2\left(x+1\right)^2=3\left(7-y^2\right)\)
Do \(\left(x+1\right)^2\ge0\Rightarrow7-y^2\ge0\) \(\Rightarrow y^2\le7\) (1)
Mà \(2\left(x+1\right)^2\) là một số tự nhiên chẵn và 3 là số lẻ
\(\Rightarrow7-y^2\) là một số chẵn \(\Rightarrow y^2\) là một số lẻ (2)
Từ (1); (2) \(\Rightarrow y^2\) là số chính phương lẻ và nhỏ hơn 7
\(\Rightarrow y^2=1\Rightarrow y=\pm1\)
\(\Rightarrow2\left(x+1\right)^2=3\left(7-1\right)=18\)
\(\Rightarrow\left(x+1\right)^2=9\)
\(\Rightarrow\left[{}\begin{matrix}x+1=3\\x+1=-3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)
-
-
-
-
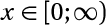
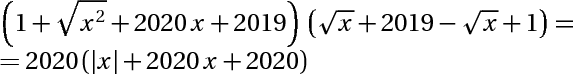
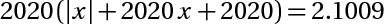
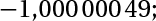
Kết quả: Giải phương trình với tập xác địnhTập xác định của phương trình
Biến đổi vế trái của phương trình
Phương trình thu được sau khi biến đổi
Lời giải thu được
Cái này tui search mạng nhá