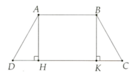
Cho hình thang cân ABCD (AB // CD )
Biết AB = 14cm
CD = 24cm
Chiều cao AH = 12cm
Tính chu vi và diện tích của hình thang ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
28 tháng 6 2018
kẻ 1 đg vuông góc từ B cắt DC tại K
xét tg ADH và tg BCK :
góc AHD= góc BKC ( = 90 độ )
AD= BC ( gt )
góc ADH= góc BCK ( gt )
=> tg ADH= tg BCK ( ch- gn)
=> DH= KC ( 2 cạnh t/ứ ) ( 1)
vì AB song song DC=> ABKD là hcn ( tự chứng minh)
=> AB=Dk= 8 cm
=> DH= KC= (DC-DK ) :2= 3 cm
áp dụng đlí pi-ta-go cho tg ADH vuông ở H :
AH2+DH2= AD2
TS : AH2= 52-32
=> AH = 4 cm
CM
4 tháng 1 2020
a) Chứng minh
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2
VÌ hình thang cân
=> AC= BD
Kẻ đường cao BK của hình thang ta co
HK=AB= 14cm
=> KD=CH=(24-14):2=5 cm
Tam giác ACH vuông tại H có
\(AC^2=CH^2+AH^2\) ( định lý Py- ta -go )
\(AC^2=5^2+12^2\)
AC=13cm
Chu vi hình thang là AB+BD+AC+DC =14+24+13+13=64cm
Diện tích hình thang là
S=\(\frac{\left(14+24\right)\times12}{2}=228cm^2\)