Cm rằng Tổng 2 cạnh bên của 1 hình thang lớn hơn hiệu 2 đáy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vẽ hình thang ABCD nối B với D(AB//CD)
Áp dụng BĐT tam giác ta có:
BD+AB>AD
BD+CD>BC
Trừ vế với vế ta được:
BD+CD-BD-AB>BC-AD
=>CD-AB>BC-AD
=>ĐPCM
kẻ be song song với ad thì ad= be, ab= de
ta có ad+bc=be+bc
cd-ab= cd-de=ec xét tam giác bec ta có
be+bc>ec nên da+bc>cd-ab

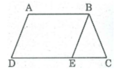
Giả sử hình thang ABCD có AB // CD
Từ B kẻ đường thẳng song song với AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song nên AB = ED và AD = BE
Ta có: CD – AB = CD – ED = EC (1)
Trong ∆ BEC ta có:
BE + BC > EC (bất đẳng thức tam giác)
Mà BE = AD
Suy ra: AD + BC > EC (2)
Từ (1) và (2) suy ra: AD + BC > CD – AB

a, Trong hình thang ABCD (AB // CD), kẻ BE // AD
Ta có: BE = AD, AB = DE (hình thang có 2 cạnh bên song song)
Xét t/g BEC có: BE + BC > EC (BĐT tam giác)
=> AD + BC > CD - DE hay AD + BC > CD - AB (đpcm)
b, Xét t/g BEC có: EC < |BC - BE|
=> CD - AB < |BC - AD| (đpcm)
c,Kẻ BF // AC
=> AB = CF ; AC = BF (hình thang có 2 cạnh bên song song)
Xét t/g BDF có: BD + BF > DF (BĐT tam giác)
=> BD + AC > DF
=> BD + AC > DC + CF
=> BD + AC > DC + AB (đpcm)


Vẽ hình thang ABCD nối B với D
Áp dụng bất đăng thức tam giác được:
BD + AB > AD (1)
BD + CD > BC (2)
Lấy (2) trừ (1) ta được:
BD + CD - BD - AB > BC - AD
\(\Leftrightarrow\) CD - AB > BC - AD
kẻ hình thang ABCD
kẻ 2 đường cao AH và BK nối B với H
xét tam giác ABH và tam giác KBH
có ^ABH = ^KBH ( 2gocs so le trong )
HB chung
=> tam giác ABH = tam giác KBH (cạnh huyền +góc nhọn )
=> AB =HK ( 2 cạnh tương ứng )
xét tam giác BKC có BC>KC ( trong tam giác vuông cạnh huyền là cạnh lớn nhất )(1)
xét tam giác AHD có AD>HD (trong tam giác vuông cạnh huyền là cạnh lớn nhất)(2)
từ (1) và (2) => BC+AD >KC+HD
ta lại có DH+DK +HK =DC
mà AB=HK (C/m )
=> DH+DK+AB =dc
ta có DC-AB = DH+DK+AB-AB= DH+DK
mà DH+DK<BC+AD(c/m)
=>DC -AB< BC+AD
vậy tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy


Vẽ hình thang ABCD nối B với D(AB//CD)
Áp dụng BĐT tam giác ta có:
BD+AB>AD
BD+CD>BC
Trừ vế với vế ta được:
BD+CD-BD-AB>BC-AD
=>CD-AB>BC-AD
=>ĐPCM

#)Giải :
Nối B với D (AB//CD)
Áp dụng bất đẳng thức, ta có:
BD + AB > AD
BD + CD > BC
Trừ hai vế với nhau, ta được: BD + CD - BD - AB > BC - AD
=> CD - AB > BC - AD => đpcm
Đây nè bạn hiền (nhớ nhìn hình vẽ mình nha):
Đầu tiên để dễ quan sát ta vẽ 1 hình thang (đặt là ABCD cho gọn) với 2 đáy AB song song CD . Sau đó nối B với C :)
Ta có : Tổng của 2 cạnh trong tam giác luôn lớn hơn cạnh còn lại (Bất Đẳng Thức Trong Tam Giác)
Từ đó suy ra: BC + AB > AC hay AC < BC + AB
BC + CD > CD hay CD < BC + CD
Nên CD - AC < BC + AB - (BC + CD) = BC + AB - BC - CD = AB - CD
Vậy ta có được điều cần chứng minh