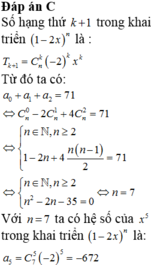Bài 6: Cho đa thức f(x) với các hệ số nguyên : f(x) = anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0. Chứng minh rằng nếu đa thức có nghiệm hữu tỉ \(\frac{p}{q}\) ( tốigiản) thì P là ước của a0; q là ước của an
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 4 2019
f(x) = anxn + an – 1xn– 1 + … + a1x + ao
+
g(x) = bnxn + bn – 1xn– 1 + … + b1x + bo
--------------------------------------------------------
f(x) + g(x) = (an + bn)xn + (an – 1 + bn – 1)xn– 1 + ….. + (a1 + b1)x + (ao + bo)
CM
6 tháng 8 2017
f(x) = anxn + an – 1xn– 1 + … + a1x + ao
-
g(x) = bnxn + bn – 1xn– 1 + … + b1x + bo
--------------------------------------------------------
f(x) - g(x) = (an - bn)xn + (an– 1 - bn – 1)xn– 1 + ..… + (a1 - b1)x + (ao - bo)
CM
18 tháng 3 2017
Chọn D
Đạo hàm hai vế f(x)
Số hạng tổng quát thứ k + 1 trong khai triển thành đa thức của 
CM
19 tháng 10 2017
Đáp án A
Theo đề ta có 1 + 2 x n = a 0 + a 1 x + .... + a n x n .
Thay x = 1 2 ta có 1 + 1 n = a 0 + a 1 2 + a 2 2 2 + ... + a n 2 n = 4096 .
⇔ 2 n = 4096 ⇔ n = 12
Hệ số của số hạng tổng quát trong khai triển nhị thức 1 + 2 x 12 là a n = C 12 n .2 n ; a n − 1 = C 12 n − 1 .2 n − 1
Xét bất phương trình với ẩn số n ta có C 12 n − 1 .2 n − 1 ≤ C 12 n .2 n .
⇔ 12 ! n − 1 ! . 13 − n ! ≤ 12 ! .2 n ! . 12 − n ! ⇔ 1 13 − n ≤ 2 n ⇔ n ≤ 26 3
Do đó bất đẳng thức đúng với n ∈ 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 và dấu đẳng thức không xảy ra.
Ta được a 0 < a 1 < a 2 < ... < a 8 và a 8 > a 9 > a 10 > a 11 > a 12 .
Vậy giá trị lớn nhất của hệ số trong khai triển nhị thức là C 12 8 .2 8 = 126720 .
CM
25 tháng 10 2019
Ta có
1 C n 2 + 7 C n 3 = 1 n ⇔ n ≥ 3 2 n n - 1 + 7 . 3 ! n n - 1 n - 2 = 1 n ⇔ n ≥ 3 n 2 - 5 n - 36 = 0 ⇔ n = 9
Suy ra a 8 là hệ số của x 8 trong khai triển 8 1 - x 8 + 9 1 - x 9
Vậy ta thu được a 8 = 8 . C 8 8 + 9 . C 9 8 = 89
Đáp án C
