 hộ em với
hộ em với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số sản phẩm dự định là a (sản phẩm ) (a là số tự nhiên khác 0)
Vì theo dự định mỗi ngày sản xuất 50 sản phẩm nên số ngày theo dự định là \(\dfrac{a}{50}\)
Nhưng thực tế , đội đã sản xuất theeo được 30 sản phẩm do mỗi ngày vượt mức 10 sản phẩm (nghĩa là sản xuất 60 sản phẩm) , nên số ngày thực tế là \(\dfrac{a+30}{60}\)
Vì thực tế sớm hơn dự định 2 ngày nên ta có phương trình :
\(\dfrac{a}{50}=\dfrac{a+30}{60}+2\\ \Leftrightarrow6a=5\left(a+30+120\right)\\\Leftrightarrow a=750\left(t.m\right) \)
Vậy số sản phẩm dự định là 750 sản phẩm
Bài 3:
Gọi số sản phẩm đội phải sản xuất theo kế hoạch là x( sản phẩm, x\(\in N\)*)
Thời gian đội sản xuất theo kế hoạch là: \(\dfrac{x}{50}\) (ngày)
Số ngày làm thực tế là: \(\dfrac{x+30}{50+10}=\dfrac{x+30}{60}\) (ngày)
Theo bài ra, ta có phương trình:
\(\dfrac{x}{50}-\dfrac{x+30}{60}=2\)
\(\Leftrightarrow\dfrac{60x-50\left(x+30\right)}{50.60}=2\)
\(\Leftrightarrow60x-50x-1500=6000\Leftrightarrow x=750\)(thoả mãn)
Vậy theo kế hoạch đội phải sản xuất 750 sản phẩm

a) \(P=U.I\Rightarrow I=\dfrac{P}{U}=\dfrac{75}{220}=\dfrac{15}{44}\left(A\right)\)
b) \(A=P.t=75.30.4.60.60=32400000\left(J\right)=9\left(kWh\right)\)
c) Tiền điện phải trả: \(9.2000=18000\left(đồng\right)\)

vì ít hơn anh 10 tuổi nên em hiện nay đang là 10 tuổi

Câu này chỉ có tính máy:
12345678987654321.11 = 1.358024689x1017


\(R_1nt\left(R_2//R_3\right)\)
a)\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{20\cdot20}{20+20}=10\Omega\)
\(R_m=R_1+R_{23}=10+10=20\Omega\)
b)\(I_m=I_{23}=I_1=0,4A\)
\(U_1=R_1\cdot I_1=10\cdot0,4=4V\)
\(U_{23}=R_{23}\cdot I_{23}=10\cdot0,4=4V\)
Có \(R_2//R_3\Rightarrow U_2=U_3=U_{23}=4V\)
\(R_m=R_1+\dfrac{R_2.R_3}{R_2+R_3}=10+\dfrac{20.20}{20+20}=20\left(\Omega\right)\)
\(I=I_1=I_{23}=0,4\left(A\right)\)
\(U_1=I_1.R_1=0,4.10=4\left(V\right)\)
\(U_{23}=U_2=U_3=I_{23}.R_{23}=0,4.\dfrac{20.20}{20+20}=4\left(V\right)\)

\(a,\dfrac{6.12-6.7}{60}=\dfrac{6\left(12-7\right)}{60}=\dfrac{6.5}{60}=\dfrac{30}{60}=\dfrac{1}{2}\\ b,\dfrac{35.18-35}{\left(-34\right).7}=\dfrac{35\left(18-1\right)}{\left(-34\right).7}=\dfrac{35.17}{\left(-34\right).7}=\dfrac{595}{-238}=\dfrac{-5}{2}\)
\(c,\dfrac{42-11.42}{21.\left(-15\right)}=\dfrac{42\left(1-11\right)}{21.\left(-15\right)}=\dfrac{2.21.\left(-10\right)}{21.\left(-15\right)}=\dfrac{-20}{-15}=\dfrac{4}{3}\)

Vì x,y,z>0 nên áp dung bất đẳng thức Cô-si ta có:
\(\dfrac{1}{x^2+2yz}\)+\(\dfrac{1}{y^2+2xz}\)+\(\dfrac{1}{z^2+2xy}\)≥\(\dfrac{\left(1+1+1\right)^3}{x^2+y^2+z^2+2xy+2yz+2xz}\)
mà x+y+z=1 ⇔ x2+y2+z2+2xy+2yz+2zx=1 (bình phương cả 2 vế)
nên \(\dfrac{1}{x^2+2yz}\)+\(\dfrac{1}{y^2+2xz}\)+\(\dfrac{1}{z^2+2xy}\)≥\(\dfrac{\left(1+1+1\right)^2}{\left(x+y+z\right)^2}\)=9



 Ai đó giải hộ em với em bài này với ạ (nếu rảnh)
Ai đó giải hộ em với em bài này với ạ (nếu rảnh)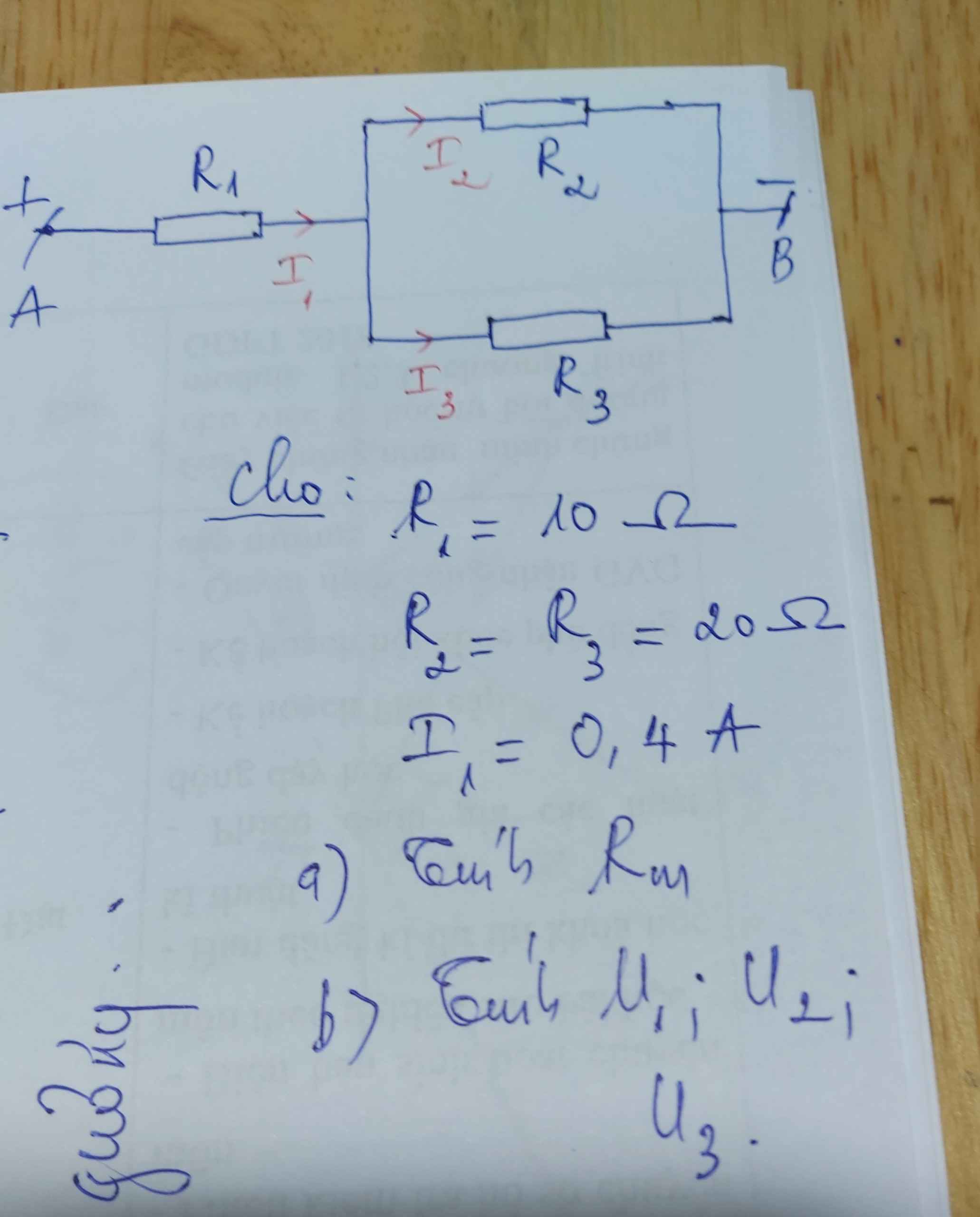
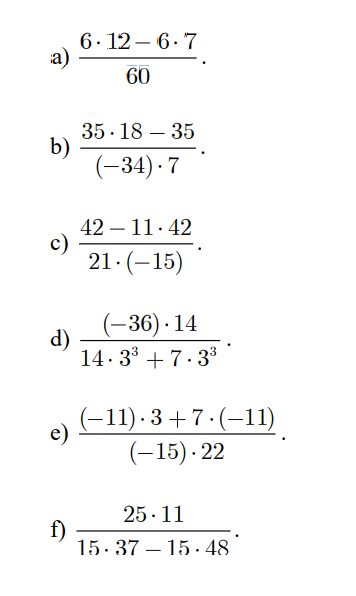 làm hộ em với ạ em đg gấp
làm hộ em với ạ em đg gấp 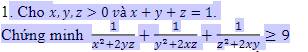 ai làm hộ em với em cần gấp;-;
ai làm hộ em với em cần gấp;-;

