Cho tích phân \(\int_0^4\frac{x}{4+2\sqrt{x+1}}dx\)=\(\frac{a}{3}\)+ bln2 +cln3 với a,b,c là sô nguyên. Tính tổng S= a+ b+c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(I_1=3\int_1^2x^2dx+\int_1^2\cos xdx+\int_1^2\frac{dx}{x}=x^3\)\(|^2 _1\)+\(\sin x\)\(|^2_1\) +\(\ln\left|x\right|\)\(|^2_1\)
\(=\left(8-1\right)+\left(\sin2-\sin1\right)+\left(\ln2-\ln1\right)\)
\(=7+\sin2-\sin1+\ln2\)
b) \(I_2=4\int_1^2\frac{dx}{x}-5\int_1^2x^4dx+2\int_1^2\sqrt{x}dx\)
\(=4\left(\ln2-\ln1\right)-\left(2^5-1^5\right)+\frac{4}{3}\left(2\sqrt{2}-1\sqrt{1}\right)\)
\(=4\ln2+\frac{8\sqrt{2}}{3}-32\frac{1}{3}\)

a.
Đặt \(\sqrt{1-x^2}=u\Rightarrow x^2=1-u^2\Rightarrow xdx=-udu\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=1\\x=1\Rightarrow u=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_1\left(1-u^2\right).u.\left(-udu\right)=\int\limits^1_0\left(u^2-u^4\right)du=\left(\dfrac{1}{3}u^3-\dfrac{1}{5}u^5\right)|^1_0\)
\(=\dfrac{2}{15}\)
b.
\(\int\limits^2_1\dfrac{dx}{x^2-2x+2}=\int\limits^2_1\dfrac{dx}{\left(x-1\right)^2+1}\)
Đặt \(x-1=tanu\Rightarrow dx=\dfrac{1}{cos^2u}du\)
\(\left\{{}\begin{matrix}x=1\Rightarrow u=0\\x=2\Rightarrow u=\dfrac{\pi}{4}\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^{\dfrac{\pi}{4}}_0\dfrac{1}{tan^2u+1}.\dfrac{1}{cos^2u}du=\int\limits^{\dfrac{\pi}{4}}_0\dfrac{cos^2u}{cos^2u}du=\int\limits^{\dfrac{\pi}{4}}_0du\)
\(=u|^{\dfrac{\pi}{4}}_0=\dfrac{\pi}{4}\)

Đáp án C.
I = ∫ 0 ln 6 e x 1 + e x + 3 d x.
Đặt
t = e x + 3 ⇒ t 2 = e x + 3 ⇒ 2 t d t = e x d x
Đổi cận x = 0 ⇒ t = 2 x = ln 6 ⇒ t = 3 . khi đó
I = ∫ 2 3 2 t d t 1 + t = 2 ∫ 2 3 1 − 1 1 + t d t = 2 t − ln t + 1 2 3 = 2 − 4 ln 2 + 2 ln 3
Do đó T = a + b + c = 2 − 4 + 2 = 0 .

Chọn C.
x 2 - x - 2 x - 1 = 0 ⇔ x + 1 x - 2 x - 1 = 0 ⇔ [ x = - 1 x = 2 D o x ∈ - 2 ; 0 ⇒ x = - 1
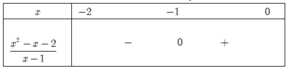
Khi đó
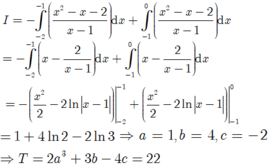

Chọn B
Đặt u = ln ( x + 1 ) d v = d x
⇒ d u = 1 x + 1 d x v = x + 1
Khi đó
∫ 1 2 ln ( x + 1 ) d x = ( x + 1 ) ln ( x + 1 ) 1 2 - ∫ 1 2 d x = 3 ln 3 - 2 ln 2 - 1
Vậy a=3; b=-2; c=-1 ⇒ S = a + b + c = 0
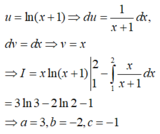
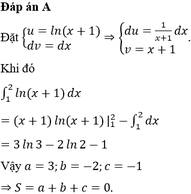
Đặt \(\sqrt{x+1}=t\Rightarrow x=t^2-1\Rightarrow dx=2t.dt\)
\(\left\{{}\begin{matrix}x=0\Rightarrow t=1\\x=4\Rightarrow t=\sqrt{5}\end{matrix}\right.\)
Chà, cận xấu, đề là \(2\sqrt{x+1}\) hay \(\sqrt{2x+1}\) bạn? Nghi ngờ đoạn này
Đề mẫu là 2\(\sqrt{x+1}\)b ạ