Trong tất cả các tam giác có cùng chiều dài một cạnh là a và có cùng chiều cao tương ứng với cạnh ấy là h. Hãy tìm tam giác có bán kính đường tròn nội tiếp trong tam giác ấy là lớn nhất
help me!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)

Bài 1 :
Nửa chu vi hình chữ nhật là: 50:2=25 (m)
Gọi chiều rộng là x (0<x<12,5)
=> chiều dài là: 25 -x (m)
Diện tích là: x (25-x)
Ta có phương trình:
\(x\left(25-x\right)=144\)
\(\Rightarrow-x^2+25x=144\)
\(\Rightarrow x^2-25x+144=0\)
\(\Rightarrow x^2-9x-16x+144=0\)
\(\Rightarrow\left(x-9\right)\left(x-16\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=9\\x=16\end{cases}}\)
Vậy chiều rộng là 9m và chiều dài là 25-9=16m

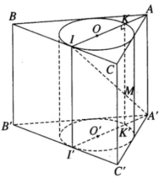
Hình trụ nội tiếp trong lăng trụ tam giác đều có đường tròn đáy tiếp xúc tại trung điểm các cạnh của tam giác đáy. Gọi I là trung điểm của cạnh BC, r là bán kính đáy của hình trụ nội tiếp trong lăng trụ
Ta có: 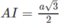
Do đó: 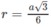
Ta có diện tích xung quanh của hình trụ nội tiếp lăng trụ là:
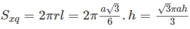

\(h=\sqrt{b^2-\frac{a^2}{4}}\Rightarrow S=\frac{1}{2}ah=\frac{1}{2}a\sqrt{b^2-\frac{a^2}{4}}\)
\(R=\frac{abb}{4S}=\frac{ab^2}{\sqrt{4b^2-a^2}.a}=\frac{b^2}{\sqrt{4b^2-a^2}}\)
\(r=\frac{S}{p}=\frac{a\sqrt{b^2-\frac{a^2}{4}}}{a+2b}\)
I donnot know
Ta có \(BC=a,AH=h\)không đổi
\(\Rightarrow S_{ABC}=\frac{ah}{2}\)không đổi
Đặt : \(S_{ABC}=S,\)Ta có:
\(S=r.\frac{AB+BC+CA}{2}=\frac{r}{2}\left(a+AB+CA\right).\)
Do đó r lớn nhất \(\Leftrightarrow a+AB+CA\)nhỏ nhất
\(\Leftrightarrow AB+CA\)nhỏ nhất
Ta có : Điểm A thuộc đường thẳng xy song song với BC cách BC một đoạn là h.
Gọi D là điểm đối xứng của B qua xy \(\Rightarrow AB=AD\)
\(\Rightarrow AB+AC=AD+AC\ge DC\)không đổi
\(min\left(AB+AC\right)=DC\)khi A trùng với A1 là giao điểm của xy và CD . Lúc đó xét \(\Delta BCD\),
ta có IA1 là đường trung bình nên :
\(A_1C=A_1D\Rightarrow A_1C=A_1B.\)Hay \(\Delta ABC\)cân.
P/S bài làm chỉ mang tính chất hướng dẫn