chứng minh rằng nếu 2 phương trình x^2 + p1x +q1 = 0 và x^2 +p2x +q2 = 0 có nghiệm chung thì (q1-q2)^2 + (p2-p1)(q2p1-q1p2)=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 5 2017
Đề mà cứ q,q,p,p nhìn mỏi mắt quá.
Sửa đề: Chứng minh rằng nếu hai phương trình \(\hept{\begin{cases}x^2+ax+b=0\\x^2+cx+d=0\end{cases}}\)
Chứng minh: \(\left(b-d\right)^2+\left(c-a\right)\left(da-bc\right)=0\)
Gọi t là nghiệm chung của 2 pt thì ta có:
\(\hept{\begin{cases}t^2+at+b=0\left(1\right)\\t^2+ct+d=0\left(2\right)\end{cases}}\)
Lấy (2) - (1) ta được
\(\left(c-a\right)t+\left(d-b\right)=0\)
\(\Leftrightarrow t=\frac{b-d}{c-a}\) thế ngược lại (1) ta được
\(\left(\frac{b-d}{c-a}\right)^2+\left(\frac{b-d}{c-a}\right)\cdot a+b=0\)
\(\Leftrightarrow\left(b^2-2bd+d^2\right)+\left(a^2d-adc+c^2b-abc\right)=0\)
\(\Leftrightarrow\left(b-d\right)^2+\left(ad\left(a-c\right)+cb\left(c-a\right)\right)=0\)
\(\Leftrightarrow\left(b-d\right)^2+\left(c-a\right)\left(cb-ad\right)=0\)
PS: Xem lại đề thử bạn. Chứ m không thấy mình nhầm chỗ nào hết.
2 tháng 5 2017
Xét 2 pt x2 - 2x + 1 = 0 và x2 - 3x + 2 = 0. 2 pt này có nghiệm chung là 1.
Ta sẽ chỉ ra là đề sai như sau:
Ta có
(q1-q2)^2+(p2-p1)(q2p1-q1p2)
= (1 - 2)2 + (-3 + 2)[2.(-2) - 1.(-3)]
= 1 + (-1).(-1) = 2
Đề sai rõ ràng nhé.
Nếu sửa lại như mình nói thì sẽ được
(q1-q2)^2+(p2-p1)(q1p2-q2p1)
= (1 - 2)2 + (-3 + 2)[1.(-3) - 2.(-2)]
= 1 + (-1).(1) = 1 - 1 = 0
Thì mới đúng nhé
17 tháng 6 2021
Giả sử 2 pt vô nghiệm. Khi đó \(p_1^2< 4q_1;p_2^2< 4q_2\Rightarrow p_1^2+p_2^2< 4\left(q_1+q_2\right)\le2p_1p_2\Leftrightarrow\left(p_1-p_2\right)^2< 0\). (vô lí)
Do đó tồn tại 1 pt có nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 5 2020
\(\Delta_1=p_1^2-4q_1\) ; \(\Delta_2=p_2^2-4q_2\)
Ta có:
\(\Delta_1+\Delta_2=p_1^2+p_2^2-4\left(q_1+q_2\right)=p_1^2+p_2^2-2p_1p_2=\left(p_1-p_2\right)^2\ge0\) với mọi \(p_1;p_2\)
\(\Rightarrow\) Luôn tồn tại ít nhất 1 trong 2 giá trị \(\Delta_1\) hoặc \(\Delta_2\) ko âm
\(\Rightarrow\) Ít nhất 1 trong 2 pt luôn có nghiệm
CM
6 tháng 4 2017
Đáp án B
Phương pháp
Phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng ( Q 1 ) và ( Q 2 ) là mặt phẳng song song và nằm chính giữa ( Q 1 ) và ( Q 2 )
Cách giải
Phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng ( Q 1 ) và ( Q 2 ) là mặt phẳng song song và nằm chính giữa ( Q 1 ) và ( Q 2 )
Ta có
VT
3 tháng 11 2018
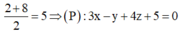
Đáp án: A
Vì cường độ điện trường tại M bằng 0 nên hai vecto E 1 do q1 gây ra và E 2 do q2 gây ra phải ngược chiều và cùng độ lớn nên M nằm trên đường thẳng AB
r1 < r2 và r1 + AB = r2 nên q1 và q2 trái dấu và |q1| < |q2|
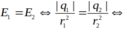
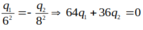
và q1 + q2 = 7.10-8
=> q1= -9.10-8 C, q2= 16.10-8 C
mik xl nha...để p.q.khó nhìn quá mik sửa lại nha...bn cứ tự thay p.q vô..
Sửa đề: Chứng minh rằng nếu 2 pt \(\hept{\begin{cases}x^2+ax+b=0\\x^2+cx+d=0\end{cases}}\)
Chứng minh:(b-d)2+(c-a).(da-bc)=0
Gọi v là nghiệm chung của 2 pt, ta có:
v2+av+b=0(1)
v2+ct+d=0(2)
Lấy (2)-(1), ta được:
(c-a)v +(d-b)=0
<=> v= \(\frac{b-d}{c-a}\)
Thay v =\(\frac{b-d}{c-a}\)vào (1), ta được:
(\(\frac{b-d}{c-a}\))2 +(\(\frac{b-d}{c-a}\))2 .a+b=0
<=> (b2-2bd+d2) +(a2d-adc+c2b-abc)=0
<=>(b-d)2 +(ad(a-c)+cd(c-a))=0
<=>(b-d)2 +(c-a).(cb-ad)=0
mik có lm sai bn thông cảm nha!!