Hai người cùng xuất phát một lúc từ hai địa điểm A và B cách nhau 60 km người thứ nhất đi xe máy từ A đến B với vận tốc v1 = 30km/h người thứ hai đi xe đạp từ B về A với vận tốc v2 = 10km/h. Hỏi sau bao lâu hai người gặp nhau và xác định vị trí gặp nhau đó coi chuyển động hai xe là đều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
21 tháng 10 2020
Trong cùng 1 khoảng thời gian vận tốc tỷ lệ thuận với quãng đường đi được
Vận tốc A-B / Vận tốc B-A = Quãng đường đi được của người xp từ A / Quãng đường đi được của người xp từ B = 30/10=3
Chia quãng đường đi được của người xp từ A thành 3 phần bằng nhau thì quãng đường đi được của người xp từ B là 1 phần
Tổng số phần bằng nhau là
3+1=4 phần
Giá trị 1 phần hay quãng đường đi được của người xp từ B là
60:4=15 km
Thời gian hai người gặp nhau kể từ lúc xp là
15:10=1,5 giờ
Vị trí gặp nhau cách B 15 km
14 tháng 12 2019
2 người cùng xuất phát một lúc và chuyển động ngược chiều nhau vậy 2 người sẽ gặp nhau sau:
\(t_{gap}=\frac{l}{v_1+v_2}=\frac{100}{40+10}=2\left(h\right)\)
Vị trí gặp nhau cách điểm A: \(2.40=80\left(km\right)\)
Đ/S
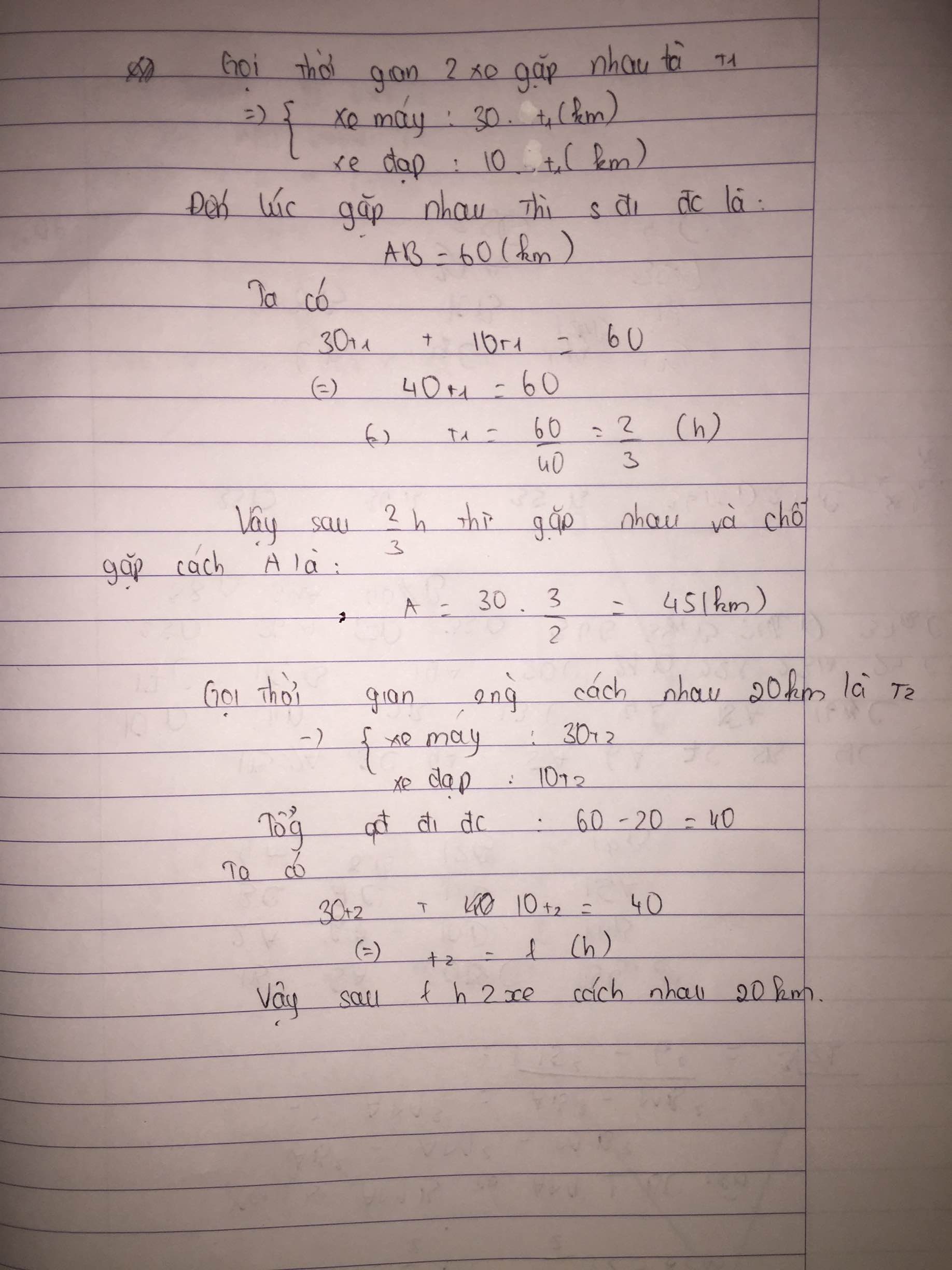
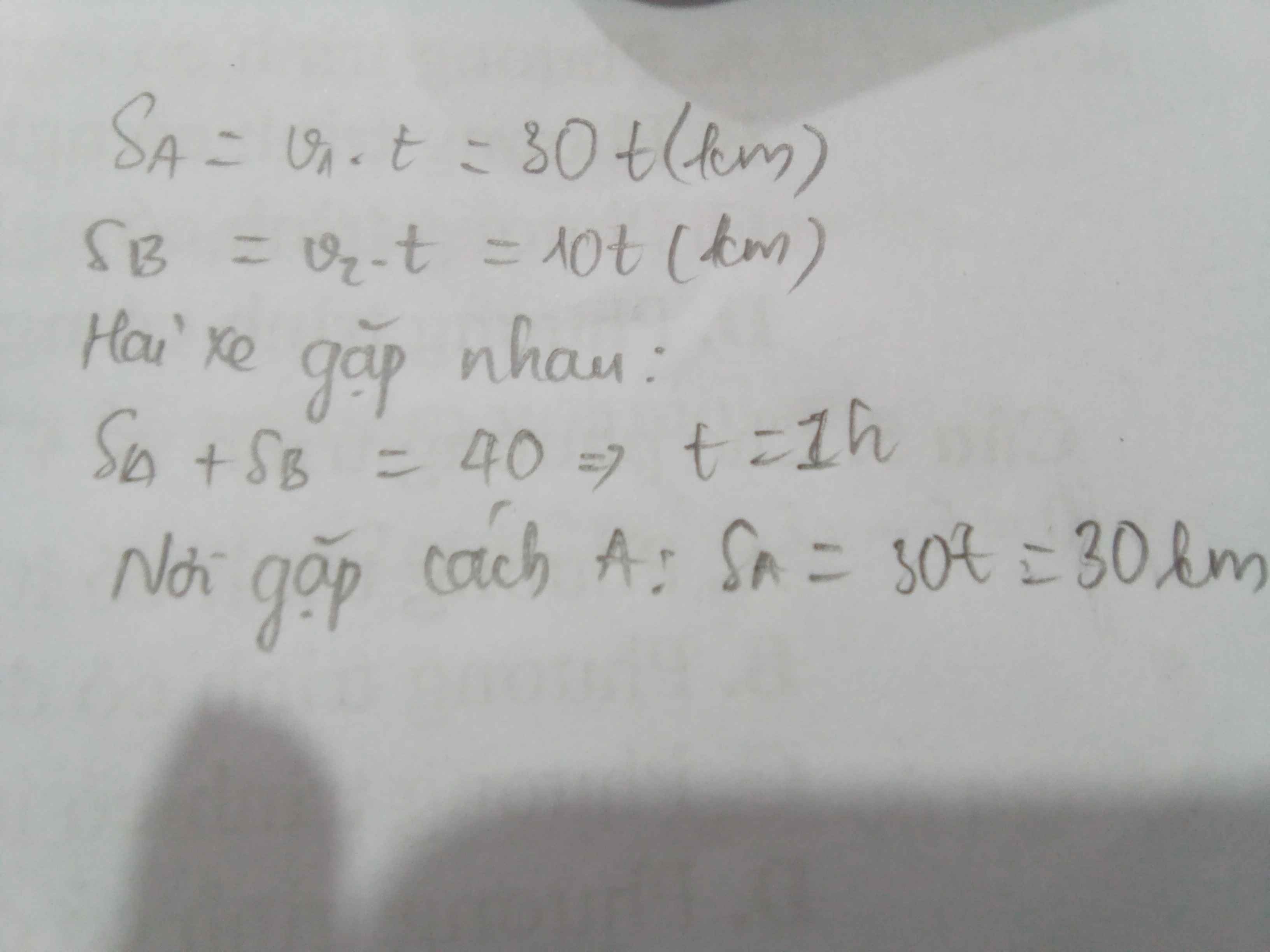
Gọi thời gian 2 xe gặp nhau là a:
Vì 2 xe đi ngược chiều nhau nên:
\(a=\frac{s}{v_1+v_2}=\frac{60}{30+10}=\frac{60}{40}=\frac{3}{2}=1,5\left(h\right)\)
Đổi 1,5 (h) = 1h30'
Vị trí gặp nhau đó cách A là:
\(L=30.1,5=45\left(km\right)\)
Gọi t (h) là thời gian hai xe gặp nhau
Do 2 xe đi ngược chiều nhau nên:
\(t=\frac{s}{v_1+v_2}=\frac{60}{30+10}=1,5\left(h\right)\)
Vị trí gặp nhau cách A là: 30.1,5=45(km)