Giải phương trình:
a.2x4-21x3+74x2-105x+50=0
b.x4-x3-10x2+2x+4=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
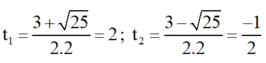
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
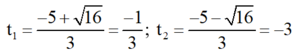
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.

2) 2x4-21x3+74x2-105x+50=0
<=>(2x4-2x3)+(-19x3+19x2)+(55x2-55x)+(-50x+50)=0
<=>2x3.(x-1)-19x2.(x-1)+55x.(x-1)-50.(x-1)=0
<=>(x-1)(2x3-19x2+55x-50)=0
<=>(x-1)[(2x3-20x2+50x)+(x2+5x-50)]=0
<=>(x-1)[2x.(x-5)2+(x2-5x+10x-50)]=0
<=>(x-1){2x.(x-5)2+[x.(x-5)+10.(x-5)]}=0
<=>(x-1)[2x.(x-5)2+(x-5)(x+10)]=0
<=>(x-1)(x-5)(2x2-10x+x+10)=0
<=>(x-1)(x-5)(2x2-5x-4x+10)=0
<=>(x-1)(x-5)[x.(2x-5)-2.(2x-5)]=0
<=>(x-1)(x-5)(x-2)(2x-5)=0
<=>x=1 hoặc x=5 hoặc x=2 hoặc x=5/2

I Don't No
~~ tk nha ~`
─(♥)(♥)(♥)────(♥)(♥)(♥) __ ɪƒ ƴσυ’ʀє αʟσηє,
──(♥)██████(♥)(♥)██████(♥) ɪ’ʟʟ ɓє ƴσυʀ ѕɧα∂σѡ.
─(♥)████████(♥)████████(♥) ɪƒ ƴσυ ѡαηт тσ cʀƴ,
─(♥)██████████████████(♥) ɪ’ʟʟ ɓє ƴσυʀ ѕɧσυʟ∂єʀ.
──(♥)████████████████(♥) ɪƒ ƴσυ ѡαηт α ɧυɢ,
────(♥)████████████(♥) __ ɪ’ʟʟ ɓє ƴσυʀ ρɪʟʟσѡ.
──────(♥)████████(♥) ɪƒ ƴσυ ηєє∂ тσ ɓє ɧαρρƴ,
────────(♥)████(♥) __ ɪ’ʟʟ ɓє ƴσυʀ ѕɱɪʟє.
─────────(♥)██(♥) ɓυт αηƴтɪɱє ƴσυ ηєє∂ α ƒʀɪєη∂,
───────────(♥) __ ɪ’ʟʟ ʝυѕт ɓє ɱє.

a) x^4 - 3x^3 + 3x - 1 = 0
<=> (x^3 - 2x^2 - 2x + 1)(x - 1) = 0
<=> (x^3 - 3x + 1)(x + 1)(x - 1) = 0
<=> x^3 - 3x + 1 khác 0 hoặc x + 1 = 0 hoặc x - 1 = 0
<=> x + 1 = 0 hoặc x - 1 = 0
<=> x = -1 hoặc x = 1

Đây là phương trình đối xứng, cách giải những bài phương trình đối xứng khác cũng giống vậy nhé!
Xét x = 0 không phải là nghiệm của phương trình
Chia cả hai vế của phương trình cho x2, ta được:
\(2x^2-21x+74-\frac{105}{x}+\frac{50}{x^2}=0\\ \Rightarrow\left(2x^2+\frac{50}{x^2}\right)-\left(21x+\frac{105}{x}\right)+74=0\\ \Rightarrow2\left(x^2+\frac{25}{x^2}\right)-21\left(x+\frac{5}{x}\right)+74=0\)
Đặt \(x+\frac{5}{x}=y\Rightarrow x^2+\frac{25}{x^2}=y^2-10\)
Thay vào phương trình, ta được:
\(2\left(y^2-10\right)-21y+74=0\\ \Rightarrow2y^2-20-21y+74=0\\ \Rightarrow2y^2-21y+54=0\\ \Rightarrow\left(2y^2-12y\right)-\left(9y-54\right)=0\\ \Rightarrow2y\left(y-6\right)-9\left(y-6\right)=0\\ \Rightarrow\left(y-6\right)\left(2y-9\right)=0\\ \Rightarrow\left(x+\frac{5}{x}-6\right)\left(2x+\frac{10}{x}-9\right)=0\\ \Rightarrow x=1;x=2\)
b) \(\Leftrightarrow x^2\left(x^2+2x-2\right)-3x\left(x^2+2x-2\right)-2\left(x^2+2x-2\right)=0\)
\(\Leftrightarrow\left(x^2-3x-2\right)\left(x^2+2x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-2=0\\x^2+2x-2=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left(x-\frac{3}{2}\right)^2=\frac{17}{4}\\\left(x+1\right)^2=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{3}{2}=\frac{\sqrt{17}}{2}\\x-\frac{3}{2}=-\frac{\sqrt{17}}{2}\\x+1=\sqrt{3}\\x+1=-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{3+\sqrt{17}}{2}\\x=\frac{3-\sqrt{17}}{2}\\x=\sqrt{3}-1\\x=-1-\sqrt{3}\end{matrix}\right.\) ( TM )
a) Dễ thấy x = 0 không là nghỉ=ệm của pt đã cho
Chia cả 2 vế của pt cho \(x^2\ne0\) ta đc :
\(2x^2-21x+74-\frac{105}{x}+\frac{50}{x^2}=0\)
\(\Leftrightarrow2\left(x^2+\frac{25}{x^2}+10\right)-21\left(x+\frac{5}{x}\right)+54=0\)
\(\Leftrightarrow2\left(x+\frac{5}{x}\right)^2-21\left(x+\frac{5}{x}\right)+54=0\)
\(\Leftrightarrow2t^2-21t+54=0\) ( với \(t=x+\frac{5}{x}\) )
\(\Leftrightarrow\left(2t-9\right)\left(t-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=\frac{9}{2}\\t=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+\frac{5}{x}=\frac{9}{2}\\x+\frac{5}{x}=6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-\frac{9}{2}x+5=0\\x^2-6x+5=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left(x-\frac{9}{4}\right)^2=\frac{1}{16}\\\left(x-1\right)\left(x-5\right)=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-\frac{9}{4}=\frac{1}{4}\\x-\frac{9}{4}=-\frac{1}{4}\\x-1=0\\x-5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\frac{5}{2}\\x=2\\x=1\\x=5\end{matrix}\right.\) ( TM )
Vậy tập nghiệm của pt đã cho là \(S=\left\{\frac{5}{2};2;1;5\right\}\)