Cho x và y là 2 số thỏa mãn đồng thời: x>= 0, y>=0, 2x+y<=4. Tìm GTLN của biểu thức: K= x^2-2x -y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
6 tháng 6 2019
Từ \(0\le x\le y\le1\) và \(2x+y\le2\Rightarrow2x^2+xy\le2x\)(nhân cả 2 vế với \(x\ge0\))
\(\left(y-x\right)y\le y-x\)(nhân cả 2 vế của \(0\le y\le1\)với \(y-x\ge0\)(do \(x\le y\))
Cộng từng vế ta có :
\(2x^2+xy+\left(y-x\right)y\le2x+y-x\)
\(\Leftrightarrow2x^2+y^2\le x+y\)
\(\Leftrightarrow\left(2x^2+y^2\right)^2\le\left(x+y\right)^2\)
Mặt khác \(\left(x+y\right)^2=\left(\frac{1}{\sqrt{2}}.\sqrt{2}x+1.y\right)^2\le\left(\frac{1}{2}+1\right)\left(2x^2+y^2\right)\)(bất đẳng thức Bunhiacopxki)
\(\Rightarrow\left(2x^2+y^2\right)^2\le\frac{3}{2}\left(2x^2+y^2\right).\)
\(\Leftrightarrow2x^2+y^2\le\frac{3}{2}.\)(đpcm)
Chúc học tốt
MT
1
31 tháng 8 2021
Ta có: \(\dfrac{x-1}{2}=\dfrac{y+1}{3}=\dfrac{z-3}{5}\)
nên \(\dfrac{2x-2}{4}=\dfrac{y+1}{3}=\dfrac{z-3}{5}\)
mà 2x+y-z=0
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x-2}{4}=\dfrac{y+1}{3}=\dfrac{z-3}{5}=\dfrac{2x+y-z-2+1+3}{4+3-5}=\dfrac{2}{2}=1\)
Do đó: x=3; y=2; z=8
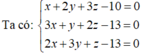
Ta cá:\(K=x^2-2\times x-y=x^2-\left(2\times x+y\right)\)
Để K đạt GTLN
Suy ra x^2 lớn nhất nên x lớn nhất
2x+y nhỏ nhất nên y nhỏ nhất(2x Ko nhỏ nhất vi x lớn nhất nên 2x lớn nhất)
Mà \(y\ge0\)
Ta chọn y=0,thay vào 2x+y ta đc
\(2\times x+0\le4\)
\(\Rightarrow2\times x\le4\)
\(\Rightarrow x\le2\)
Mà x lớn nhất nên ta chọn x=2 do đá k sẽ bằng
\(K=2^2-2\times2-0=4-4=0\)
Vậy K đạt GTLN là 0 tại x =2 và y=0
nhớ h cho mk nha