Cho em hỏi hai câu này làm như thế nào ạ?
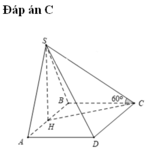
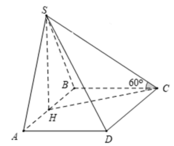
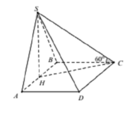
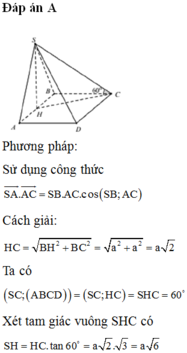
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a.Hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy là trung điểm Ab, góc giữa SC và mặt phẳng đáy bằng \(60^0\).Tính cosin góc giữa hai đường thẳng SB và AC.
Câu 2: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta\) đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng Oxy, cách đường thẳng \(\Delta\) một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.

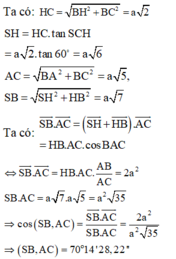
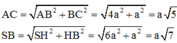
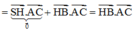
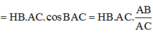

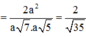
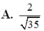
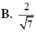
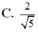
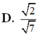
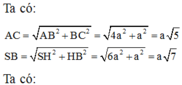
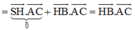
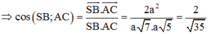
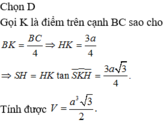
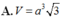
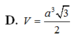

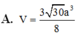
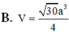
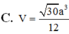
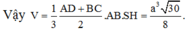



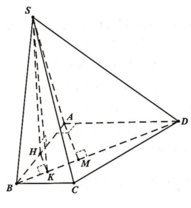
Câu 1:
Lời khuyên là nếu học lớp 12 thì tốt nhất là tọa độ hóa.
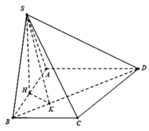
Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\left(\frac{AB}{2}\right)^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow SH=CH.tan60^0=a\sqrt{6}\)
Đặt hệ trục tọa độ Oxyz vào hình chóp, tâm O trùng H, Ox trùng toa OB, Oy trùng tia HM với M là trung điểm CD, Oz trùng tia HS, a bằng 1 đơn vị độ dài
Ta được các tọa độ: \(S\left(0;0;\sqrt{6}\right);B\left(1;0;0\right);A\left(-1;0;0\right);C\left(1;1;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{SB}=\left(1;0;-\sqrt{6}\right)\\\overrightarrow{AC}=\left(2;1;0\right)\end{matrix}\right.\) \(\Rightarrow cos\left(SB;AC\right)=\frac{\left|\overrightarrow{SB}.\overrightarrow{AC}\right|}{\left|\overrightarrow{SB}\right|.\left|\overrightarrow{AC}\right|}=\frac{2\sqrt{35}}{35}\)
Câu 2:
\(\overrightarrow{u_{\Delta}}=\overrightarrow{OI}=\left(0;1;1\right)\) ; \(\overrightarrow{n_{Oxy}}=\left(0;0;1\right)\)
Gọi \(\alpha\) là góc tạo bởi \(\Delta\) và Oxy thì \(sin\alpha=\frac{\left|\overrightarrow{u_{\Delta}}.\overrightarrow{n_{Oxy}}\right|}{\left|\overrightarrow{u_{\Delta}}\right|.\left|\overrightarrow{n_{Oxy}}\right|}=\frac{\sqrt{2}}{2}\)
Tới đây, nếu ta đặt tọa độ và tính toán thì rất dài và khó, nhưng sử dụng kiến thức hình học không gian để đơn giản hóa bài toán thì nó sẽ rất dễ.
Trong không gian, tập hợp các điểm cách đều một đường thẳng d cho trước 1 khoảng không đổi \(r\) là hình trụ nhận đường thẳng d làm trục và có bán kính \(r\)
\(\Rightarrow\) Tập hợp các điểm nằm trên Oxy cách đều \(\Delta\) chính là thiết diện cắt bởi hình trụ và mặt phẳng Oxy, đó là 1 hình elip có bán kính trục nhỏ \(a=r=6\) và bán kính trục lớn b được xác định như hình vẽ:
\(\Rightarrow b=\frac{r}{sin\alpha}=\frac{6}{\frac{\sqrt{2}}{2}}=6\sqrt{2}\)
Diện tích hình phẳng: \(S=\pi ab=36\pi\sqrt{2}\)