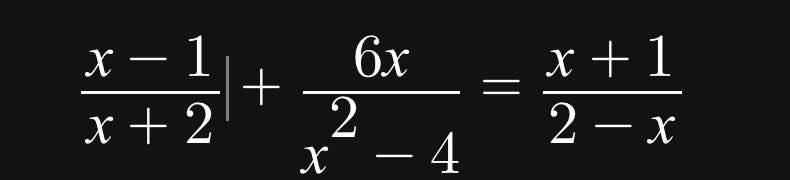Giúp em với 🥲 câu 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CB
1
27 tháng 6 2023
7:
A+B
\(=x^4-2xy+y^2+y^2+2xy+x^2+1\)
=x^4+2y^2+x^2+1
A-B
=x^4-2xy+y^2-y^2-2xy-x^2-1
=x^4-4xy-x^2-1
5:
a: =8x^2-4x^2=4x^2
b: =(5-7)*x^2y^3z^3=-2x^2y^3z^3
c: =(3+2-1/3-1/2-1/6)*x^2y^2
=4x^2y^2
29 tháng 12 2021
14: \(=\dfrac{4x+7+1}{\left(x+2\right)\left(4x+7\right)}=\dfrac{4}{4x+7}\)
KB
28 tháng 3 2022
\(lim\dfrac{2\sqrt{7n^2-2n}}{3n+2}=lim\dfrac{2\sqrt{n^2\left(7-\dfrac{2}{n}\right)}}{3n+2}=lim\dfrac{2n\sqrt{7-\dfrac{2}{n}}}{n\left(3+\dfrac{2}{n}\right)}\)
\(=lim\dfrac{2\sqrt{7-\dfrac{2}{n}}}{3+\dfrac{2}{n}}=\dfrac{2\sqrt{7}}{3}\) \(=\dfrac{a\sqrt{7}}{b}\)
Suy ra : a/b = 2/3 => a - b = -1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
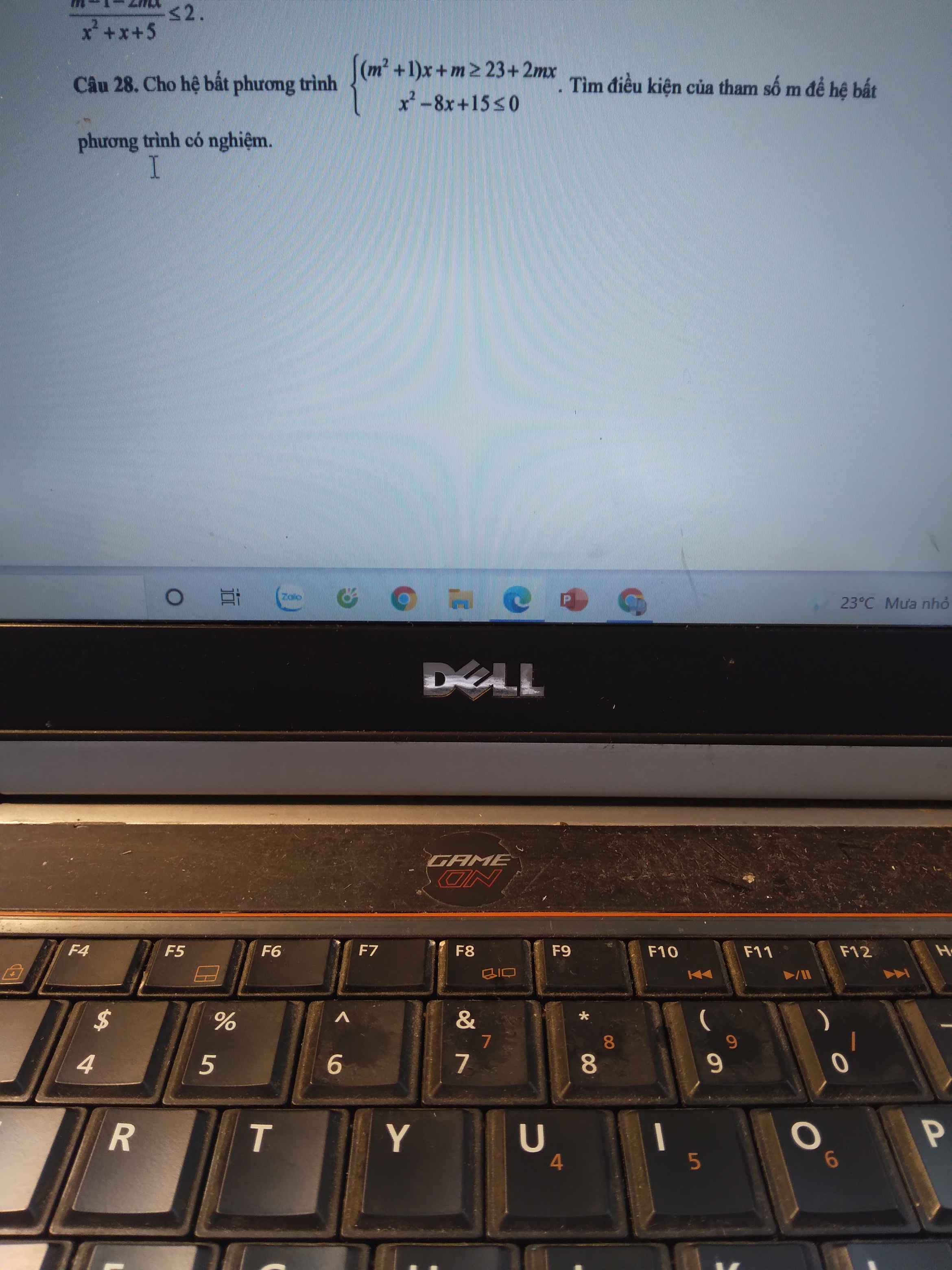
Xét BPT: \(x^2-8x+15\le0\Leftrightarrow3\le x\le5\Rightarrow D_1=\left[3;5\right]\)
Xét BPT: \(\left(m^2+1\right)x+m\ge23+2mx\)
\(\Leftrightarrow\left(m^2-2m+1\right)x\ge23-m\)
\(\Leftrightarrow\left(m-1\right)^2x\ge23-m\) (1)
- Với \(m=1\Rightarrow\left(1\right)\) trở thành \(0\ge22\) (vô lý) \(\Rightarrow\left(1\right)\) vô nghiệm (loại)
- Với \(m\ne1\Rightarrow\left(m-1\right)^2>0;\forall m\)
\(\left(1\right)\Leftrightarrow x\ge\dfrac{23-m}{\left(m-1\right)^2}\) \(\Rightarrow D_2=\left[\dfrac{23-m}{(m-1)^2};+\infty \right)\)
Hệ đã cho có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)
\(\Rightarrow\dfrac{23-m}{\left(m-1\right)^2}\le5\)
\(\Leftrightarrow23-m\le5\left(m-1\right)^2\)
\(\Leftrightarrow5m^2-9m-18\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-\dfrac{6}{5}\end{matrix}\right.\)
Y
27 tháng 6 2023
\(\dfrac{x-1}{x+2}+\dfrac{6x}{x^2-4}=\dfrac{x+1}{2-x}\left(dkxd:x\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{x-1}{x+2}+\dfrac{6x}{\left(x-2\right)\left(x+2\right)}=-\dfrac{x+1}{x-2}\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)+6x+\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=0\)
\(\Leftrightarrow x^2-2x-x+2+6x+x^2+2x+x+2=0\)
\(\Leftrightarrow2x^2+6x+4=0\)
\(\Leftrightarrow2x^2+2x+4x+4=0\)
\(\Leftrightarrow2x\left(x+1\right)+4\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x+4\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+4=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{-1\right\}\)
