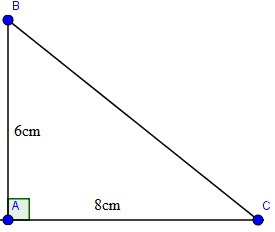
Bài4. Cho tam giác ABC có AB=6cm, AC=8cm, BC=10cm
a) Chứng minh tam giác ABC là tam giác vuông.
b) Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 8 2017
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
Suy ra: BC = 10 (cm)
18 tháng 10 2018
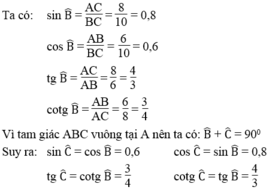
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=62+82=100BC2=AB2+AC2=62+82=100
Suy ra: BC = 10 (cm)
Ta có:
sinˆB=ACBC=810=0,8sinB^=ACBC=810=0,8
cosˆB=ABBC=610=0,6cosB^=ABBC=610=0,6
tgˆB=ACAB=86=43tgB^=ACAB=86=43
cotgˆC=tgˆB=43
2 tháng 8 2021
pytago=>\(BC=\sqrt{AB^2+AC^2}=10cm\)
\(=>\sin B=\dfrac{AC}{BC}=\dfrac{8}{10}=0,8=\cos C\)
\(=>\cos B=\dfrac{AB}{BC}=\dfrac{6}{10}=0,6=\sin C\)
\(=>\tan B=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}=\cot B\)
\(=>\cot B=\dfrac{AB}{AC}=\dfrac{3}{4}=\tan C\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(\Rightarrow sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
\(cosB=\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(tanB=\dfrac{AC}{AB}=\dfrac{4}{3}\)
\(cotB=\dfrac{AB}{AC}=\dfrac{3}{4}\)
Do tam giác ABC vuông tại A \(\Rightarrow C=90^0-B\)
\(\Rightarrow sinC=sin\left(90^0-B\right)=cosB=\dfrac{3}{5}\)
\(cosC=cos\left(90^0-B\right)=sinB=\dfrac{4}{5}\)
\(tanC=tan\left(90^0-B\right)=cotB=\dfrac{3}{4}\)
28 tháng 6 2021
Đổi AB=60mm=6cm
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có
\(\left\{{}\begin{matrix}\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\\\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\\\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\\\cot\widehat{B}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\\\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\\\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\\\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\end{matrix}\right.\)
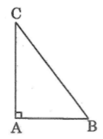
a: Xét ΔABC có
\(BC^2=AB^2+AC^2\)
hay ΔBCA vuông tại A